Wurzeln und ihre Ableitungen
Wir definieren die n-te Wurzel als die Umkehrfunktion der n-ten Potenz. Mit anderen Worten: Wenn
,
ist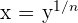 
. Wir bezeichnen die Wurzeln auch als 
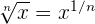. Wenn wir also die Funktion 
haben, können wir ihre Ableitung mit der Regel der Ableitung einer Potenz berechnen:
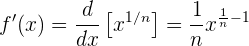
Wir beachten, dass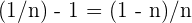 
und somit
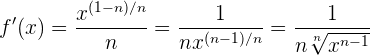
Das heißt:
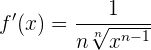
Wir denken an die Kettenregel (mit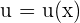 
) und erhalten
Hinweis: Du musst die Formel für die Ableitung einer Wurzel nicht auswendig kennen. Es reicht, wenn du dir 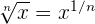merkst und dann die Regel für die Ableitung einer Potenz anwendest. Wir können jedoch Zeit bei der Berechnung von Ableitungen sparen, wenn wir die Formel auswendig können.
Hinweis: Der Spezialfall der Quadratwurtel (mit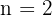 
) hat die Ableitung
Dabei handelt es sich um eine recht häufige Ableitung.
Aufgaben mit Lösungen
Berechne die Ableitung der folgenden Funktion
Um die Ableitung zu berechnen, genügt es, die Formel für die Quadratwurzel anzuwenden.
Wir stellen fest, dass 
, weshalb 
. Wenn wir also die Formel mit der Kettenregel verwenden, erhalten wir
Berechne die Ableitung der folgenden Funktion
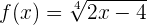
Wir wenden die Formel in Verbindung mit der Kettenregel mit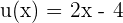 
und 
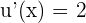an:
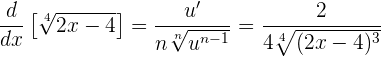
das heißt
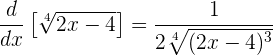
Anstatt die Formel zu verwenden, können wir mit der Funktion wie folgt arbeiten
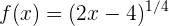
Die Ableitung wäre also
Und da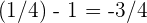 
, erhalten wir
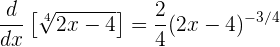
Anschließend wird die negative Potenz in den Nenner übertragen und der Bruch vereinfacht:
,
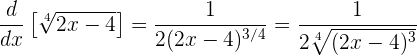was genau das gleiche Ergebnis ist, das wir zuvor erhalten hatten. Hier können wir sehen, dass es schneller geht, wenn wir die Formel für die Ableitung einer Wurzel kennen
Leite folgende Funktion ab
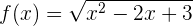
Auch hier verwenden wir die Formel zusammen mit der Kettenregel. In diesem Fall haben wir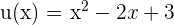 
, weshalb 
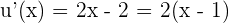. Und somit
Weshalb
Berechne die Ableitung der folgenden Funktion:
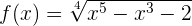
Wie in den vorangegangenen Beispielen ist es nur eine Frage der Anwendung der Formel mit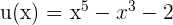 
und 
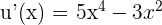. Somit
,
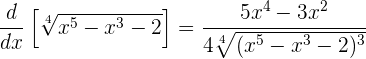was nicht mehr weiter vereinfacht werden kann.
Berechne die Ableitung der folgenden Funktion:
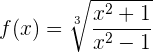
Wir stellen fest, dass der Radikand eine kompliziertere Funktion ist als die vorhergehenden Funktionen. Aus diesem Grund ist es sinnvoll, die Formel direkt zu verwenden, die Funktion aber separat abzuleiten
,
deren Ableitung durch Anwendung der Kettenregel wie folgt lautet:
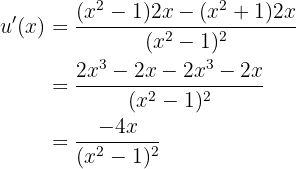
Die Ableitung ist also
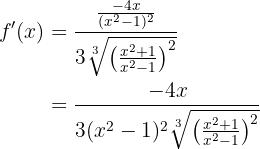
Im Anschluss stellen wir den Term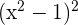 
unter die Wurzel. Deshalb müssen wir ihn in der Wurzel hoch 6 nehmen:
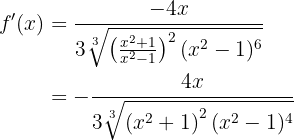
Diese ist unsere gesuchte Ableitung.
Leite folgende Funktion ab:
Wie im vorigen Fall ist es sinnvoll, zunächst die Wurzel abzuleiten:
,
deren Ableitung wie folgt ist
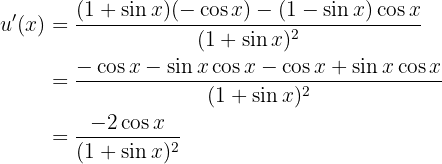
Somit lautet die Ableitung der Funktion
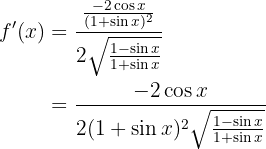
Wir schreiben den Term 
unter die Wurzel:
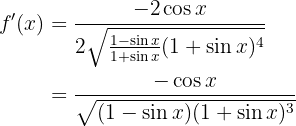
Dies ist unsere gesuchte Ableitung.
Nun können wir vereinfachen, da für den Radikanden Folgendes gilt
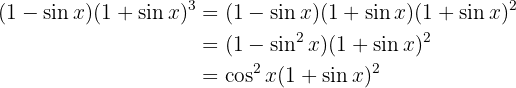
Beachte, dass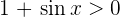 
. Wir erhalten also
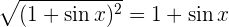
Allerding ist 
nicht immer positiv, weshalb
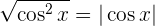
und somit
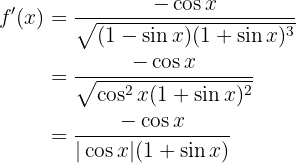
Weiter können wir nicht vereinfachen.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
