Kapitel

Ableitung der Exponentialfunktion
Die Ableitung der Exponentialfunktion ist gleich der gleichen Funktion mal dem natürlichen Logarithmus der Basis und mal der Ableitung des Exponenten.

Ableitung der Exponentialfunktion zur Basis e
Die Ableitung der Exponentialfunktion zur Basis e ist gleich der gleichen Funktion mal der Ableitung des Exponenten.

Ableitung von e hoch x
Für den speziellen Fall

gilt, dass

Nach der obigen Formel:

Daraus folgt, dass

Und somit ist die Ableitung von  :
: 
Aufgaben mit Lösung zur Ableitung

Wir haben eine Funktion der Form  , wobei
, wobei

Wir müssen nun  ableiten, da wir es für die Formel benötigen. Wir denken daran, dass
ableiten, da wir es für die Formel benötigen. Wir denken daran, dass

Die Ableitung von  ist
ist 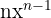 und somit lautet die Ableitung des Exponenten
und somit lautet die Ableitung des Exponenten 
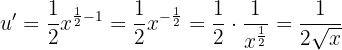
Die Formel für die Ableitung von Ausdrücken der Art  lautet
lautet
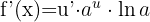
Wir setzen ein
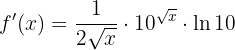

Wir haben eine Funktion der Form  , wobei
, wobei
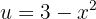
Wir leiten den Exponenten ab, da wir ihn für die Formel benötigen
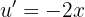
Die Formel zur Ableitung von Ausdrücken der Art  lautet
lautet
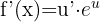
Wir setzen ein
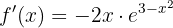

Wir haben eine Funktion der Form 
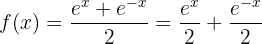
Wir leiten die Exponenten ab, da wir sie für die Formel benötigen


Die Formel für die Ableitung von Ausdrücken der Art  lautet
lautet 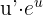 . Wir nehmen die notwendigen Substitutionen vo
. Wir nehmen die notwendigen Substitutionen vo
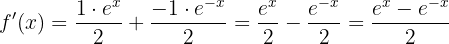
Und wenn wir keine negativen Exponenten haben möchten:
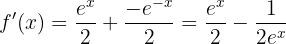

Wir haben das Produkt der Ausdrücke 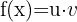


Wir leiten sie ab und beachten dabei, dass es sich beim ersten Ausdruck um eine Exponentialfunktion der Form  und beim zweiten Audsruck um
und beim zweiten Audsruck um  handelt
handelt
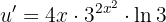
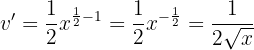
Die Formel für die Ableitung eines Produkts aus Funktionen lautet
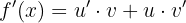
Wir setzen ein

Wir faktorisieren und vereinfachen
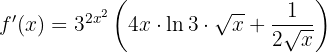

Wir haben den Quotienten der Ausdrücke  , wobei
, wobei

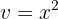
Wir leiten sie ab und beachten dabei, dass es sich bei dem ersten Ausdruck um eine Exponentialfunktion der Form  und beim zweiten Ausdruck um
und beim zweiten Ausdruck um  handelt
handelt

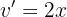
Die Formel für die Ableitung des Quotienten von Funktionen lautet

Wir setzen ein
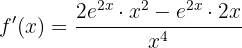
Wir faktorisieren und vereinfachen
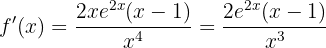

Wir haben eine Funktion der Form  , wobei
, wobei

Wir leiten  ab
ab

Die Formel für Ausdrücke der Art  lautet
lautet
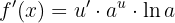
Wir setzen ein
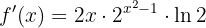

Wir haben eine Funktion der Form  , wobei
, wobei
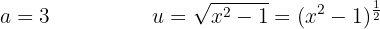
Wir leiten  ab, indem wir die Kettenregel anwenden
ab, indem wir die Kettenregel anwenden

Die Formel für Ausdrücke der Art  lautet
lautet
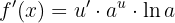
Wir setzen ein
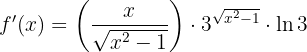
Dies ist äquivalent zu
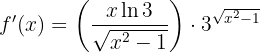

Wir haben eine Funktion der Form  , wobei
, wobei

Wir leiten  ab
ab
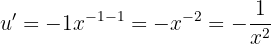
Die Formel für Ausdrücke der Art  lautet
lautet
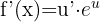
Wir setzen ein
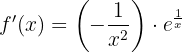
Dies ist äquivalent zu


Wir haben das Produkt der Ausdrücke 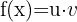

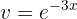
Wir leiten sie ab und beachten dabei, dass es sich beim ersten Ausdruck um einen Ausdruck der Form  handelt und der zweite Ausdruck eine Exponentialfunktion
handelt und der zweite Ausdruck eine Exponentialfunktion  ist
ist

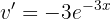
Die Formel für die Ableitung des Produkts aus Funktionen lautet
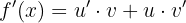
Wir setzen ein
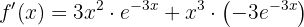
Wir faktorisieren und vereinfachen

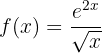
Wir haben den Quotienten der Ausdrücke  , wobei
, wobei


Wir leiten sie ab und beachten dabei, dass es sich beim ersten Ausdruck um eine Exponentialfunktion der Form  und beim zweiten Ausdruck um
und beim zweiten Ausdruck um  handelt
handelt

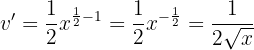
Die Formel zur Ableitung des Quotienten von Funktionen lautet

Wir setzen ein

Wir addieren im Zähler und vereinfachen

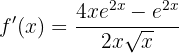
Wir faktorisieren im Zähler
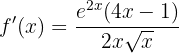
Mit KI zusammenfassen:












