Kapitel
Abstand zweier Punkte
Um mehr über den Abstand zweier Punkte zu erfahren, sehen wir uns folgende Abbildung an.
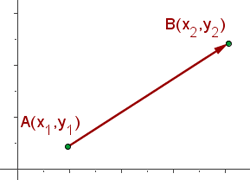
Die Abbildung zeigt zwei Punkte 
und 
in der kartesischen Ebene, die durch einen Vektor miteinander verbunden sind. Die Länge des Vektors (rot dargestellt), der die Punkte verbindet, ist der Wert, der den Abstand zwischen den Punkten und darstellt.
Formel zur Berechnung des Abstands zweier Punkte und der Satz von Pythagoras
Die Formel zur Berechung der besagten Größe ist durch den folgenden Ausdruck gegeben:
Der Wert dieser Formel kann mit Hilfe des Satzes von Pythagoras ermittelt werden. Wir betrachten dazu das rechtwinklige Dreieck mit den Eckpunkten
, und 
.
Wir stellen fest, dass der Wert der Hypotenuse dieses Dreiecks der Abstand zwischen den Punkten ist:
und .
Die Größe der Segmente, die und , und vereinen, sind jeweils 
und 
.
Der Satz von Pythagoras bestätigt, dass der Wert der Hypotenuse oder dem Abstand zwischen und wie folgt lautet: 
Beispiele für den Abstand zwischen zwei Punkten
1 Berechne den Abstand zwischen den Punkten: 
und 
2 Lege die Bedingung dafür fest, dass die Punkte 
und 
eine Einheit voneinander entfernt liegen.
Wennn der Abstand zwischen 
und 
eins ist, gilt
Wir quadrieren und eliminieren so die Wurzel
3 Beweise Folgendes: Die Punkte 
, 
und 
liegen auf einem Kreis mit dem Mittelpunkt 
.
Wenn 
der Mittelpunkt eines Kreises ist, müssen laut Definition die Abstände von nach , nach und nach 
gleich sein, damit 
und auf einem Kreis liegen. Dies überprüfen wir mithilfe der Formel für den Abstand zweier Punkte.
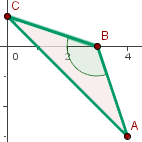
4Beschreibe das Dreieck mit folgenden Punkten: 
, 
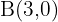und 
Zunächst berechnen wir die Abstände zwischen den Punkten des Dreiecks, um bestimmen zu können, um welche Art von Dreieck es sich handelt.
Da 
, können wir daraus schließen, dass es sich nicht um ein gleichschenkliges Dreieck handelt. Wäre dies der Fall, so wären die Abstände zwischen den einzelnen Punkten gleich.
Wenn außerdem:
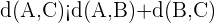, so ist das Dreieck spitzwinklig,
wenn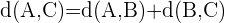 
, so ist das Dreieck rechtwinklig
und schließlich: Wenn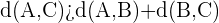 
, ist das Dreieck stumpfwinklig.
Daraus folgern wir
.
Das Dreieck ist somit stumpfwinklig.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
