Kapitel

Addition von Vektoren
Bei einer Addition von zwei oder mehreren Vektoren erhält man als Ergebnis immer einen neuen Vektor. Es gibt verschiedene Methoden, um Vektoren zu summieren: z.B. mithilfe algebraischer Rechenoperationen oder mithilfe der analytischen Geometrie.
Die algebraische Methode ist auch als direkte Methode bekannt.
In der analytischen Geometrie werden vor allem diese drei Methoden bei der Addition von Vektoren verwendet:
1. die Polygonmethode für die Addition von mehr als zwei Vektoren
2. die Dreiecksmethode für den speziellen Fall, dass nur zwei Vektoren summiert werden und
3. die Parallellogrammmethode, um ebenso zwei Vektoren zu addieren.
Algebraische Mathode
1 Direkte Methode
Um zwei oder mehrere Vektoren zu summieren, werden ihre jeweiligen Komponenten addiert.
Wenn zwei Vektoren summiert werden sollen, funktioniert das auf folgende Weise:
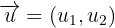
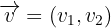
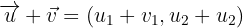
Beispiel
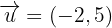
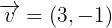
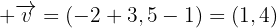
Methoden der analytischen Geometrie
1 Dreiecksmethode
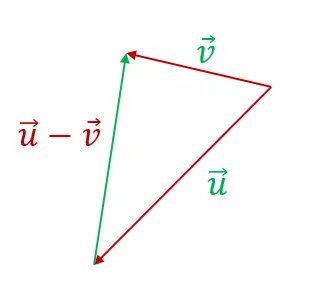
Um zwei freie Vektoren  und
und  zu summieren, werden zwei Vektoren als Repräsentanten so gewählt, dass das strong>Ende des einen mit dem strong>Startpunkt des anderen Vektors zusammenfällt.
zu summieren, werden zwei Vektoren als Repräsentanten so gewählt, dass das strong>Ende des einen mit dem strong>Startpunkt des anderen Vektors zusammenfällt.
2 Parallellogrammmethode
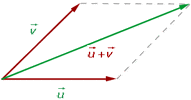
Es werden zwei Vektoren gleichen Ursprungs repräsentativ verwendet. Zu ihnen werden parallele Geraden gezogen, wodurch man ein Parallellogramm erhält, dessen Diagonale mit der Summe der Vektoren übereinstimmt.
3 Polygonmethode
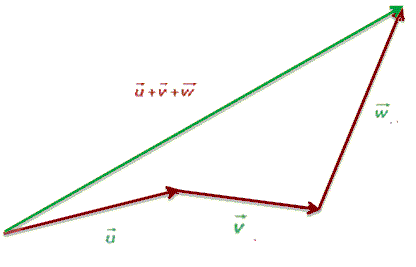
Die Polygonmethode wird verwendet, wenn mehr als zwei Vektoren summiert werden sollen. Dabei wird ein Vektor an einen anderen so angeschlossen, dass das Ende des einen mit dem Ursprung des anderen übereinstimmt, usw., bis alle Vektoren angeordnet sind. Als Ergebnis erhält man einen Vektor, der das Polygon schließt, also der, der vom Ursprung des ersten Vektors zum Endpunkt des letzten verläuft.
Subtraktion von Vektoren
Bei der Subtraktion von zwei oder mehreren Vektoren erhält man als Ergebnis einen neuen Vektor. Es gibt verschiedene Methoden, um Vektoren zu summieren: z.B. mithilfe algebraischer Rechenoperationen oder mithilfe der analytischen Geometrie.
Die algebraische Methode ist auch als direkte Methode bekannt.
In der analytischen Geometrie werden vor allem diese drei Methoden bei der Addition von Vektoren verwendet:
1. die Polygonmethode für die Subtraktion von mehr als zwei Vektoren
2. die Dreiecksmethode für den speziellen Fall, dass nur zwei Vektoren subtrahiert werden und
3. die Parallellogrammmethode, um ebenso zwei Vektoren zu subtrahieren.
Algebraische Mathode
1 Direkte Methode
Um zwei freie Vektoren 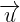 und
und 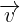 zu subtrahieren, wird
zu subtrahieren, wird 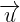 zum Gegenvektor von
zum Gegenvektor von 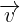 addiert.
addiert.
Die Komponenten des Gegenvektors erhält man, indem man die Komponenten der Vektoren voneinander abzieht.
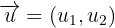
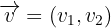
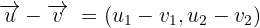
Beispiel
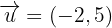
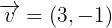
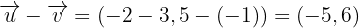
Methoden der analytischen Geometrie
1 Dreiecksmethode
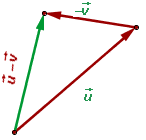
Um zwei freie Vektoren  und
und  zu subtrahieren, werden zwei Vektoren als Repräsentanten so gewählt, dass das strong>Ende des einen mit dem strong>Startpunkt des anderen Vektors zusammenfällt.
zu subtrahieren, werden zwei Vektoren als Repräsentanten so gewählt, dass das strong>Ende des einen mit dem strong>Startpunkt des anderen Vektors zusammenfällt.
2 Parallellogrammmethode
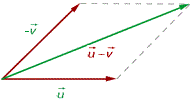
Es werden zwei Vektoren gleichen Ursprungs repräsentativ verwendet. Zu ihnen werden parallele Geraden gezogen, wodurch man ein Parallellogramm erhält, dessen Diagonale mit der Summe der Vektoren übereinstimmt.
3 Polygonmethode
Die Polygonmethode wird verwendet, wenn mehr als zwei Vektoren subtrahiert werden sollen. Dabei wird ein Vektor an einen anderen so angeschlossen, dass das Ende des einen mit dem Ursprung des anderen übereinstimmt, usw., bis alle Vektoren angeordnet sind. Als Ergebnis erhält man einen Vektor, der das Polygon schließt, also der, der vom Ursprung des ersten Vektors zum Endpunkt des letzten verläuft.
Regeln zur Addition und Subtraktion von Vektoren
1 Assoziativgesetzt
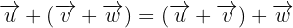
2 Kommutativgesetz
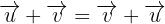
3 Neutrales Element (Nullvektor)
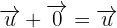
4 Inverses Element (Kehrwert)
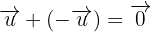
Mit KI zusammenfassen:













