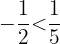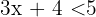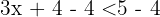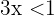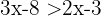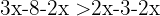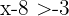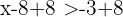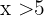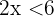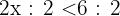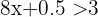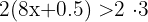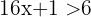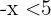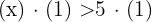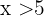Die unten genannten Eigenschaften gelten auch, wenn die strengen Ungleichungssymbole 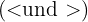 durch die entsprechenden nicht strengen Ungleichungssymbole
durch die entsprechenden nicht strengen Ungleichungssymbole 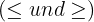 ersetzt werden.
ersetzt werden.
Transitivität
Für beliebige reelle Zahlen  und
und  :
:
- Wenn
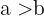 und
und 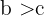 , dann
, dann 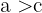 .
. - Wenn
 und
und  , dann
, dann  .
. - Wenn
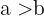 und
und 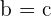 , dann
, dann 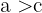 .
. - Wenn
 und
und 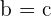 , dann
, dann  .
.
Beispiel:
- Wenn
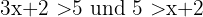 , dann
, dann 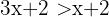

Addition und Subtraktion
Wenn die beiden Glieder einer Ungleichung um den gleichen Betrag addiert oder subtrahiert werden, ist die resultierende Ungleichung äquivalent zu der gegebenen.
Beispiele:
Multiplikation und Division
1 Durch eine positive Zahl
Wenn die beiden Glieder einer Ungleichung mit einer positiven Zahl multipliziert oder dividiert werden, ist die Ungleichung äquivalent zu der angegebenen.
Beispiele:
2 Durch eine negative Zahl
Werden die beiden Glieder einer Ungleichung mit derselben negativen Zahl multipliziert oder dividiert, so ändert die resultierende Ungleichung ihre Richtung und entspricht der gegebenen Ungleichung.
Beispiel
Gegenüberliegend
Für beliebige reelle Zahlen  und
und 
- Wenn
 , dann
, dann 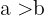 .
. - Wenn
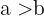 , dann
, dann  .
.
Beispiel
-
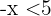 , dann
, dann 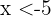
Wechselseitig
Für reelle Zahlen  und
und  ungleich Null
ungleich Null
1 Sowohl positiv als auch negativ zur gleichen Zeit:
- Wenn
 dann
dann 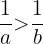
- Wenn
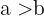 , dann
, dann 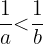
Beispiel
-
 , dann
, dann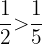
2 Wenn a und b unterschiedliche Vorzeichen haben:
- Wenn
 , dann
, dann 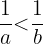
- Wenn
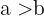 , dann
, dann 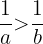
Beispiel
-
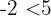 , dann
, dann