Bei der Untersuchung der analytischen Geometrie spielen Verschiebungen in der Ebene eine grundlegende Rolle. Diese Art der geometrischen Transformation ermöglicht es, Figuren oder Punkte von einer Position zu einer anderen zu bewegen, wobei ihre Form, Größe und Ausrichtung erhalten bleiben. Bei einer Verschiebung bewegt sich jeder Punkt der Figur in dieselbe Richtung und um denselben Betrag, der durch einen Verschiebungsvektor definiert ist.
In diesem Artikel stellen wir eine Reihe von Übungen zu Verschiebungen in der kartesischen Ebene vor. Anhand dieser Beispiele kann man besser verstehen, wie Verschiebungen auf verschiedene geometrische Elemente, wie Punkte, Segmente, Vielecke und komplexe Figuren, angewendet werden. Darüber hinaus wird jede Übung von einer detaillierten Erklärung begleitet, um das Verständnis zu erleichtern und die theoretischen Konzepte zu festigen.

Verschiebung in der Ebene
Eine Verschiebung in der Ebene ist durch den Vektor 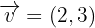 gegeben. Ermittle die Abbildung durch die Verschiebung eines Punktes
gegeben. Ermittle die Abbildung durch die Verschiebung eines Punktes 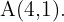
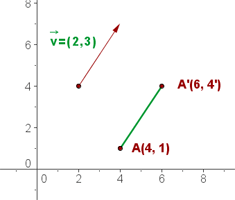
Wir denken daran, dass die Verschiebung um den Vektor 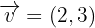 gegeben ist durch
gegeben ist durch
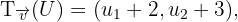
wobei 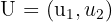 . Daher lautet die Abbildung des Vektors von
. Daher lautet die Abbildung des Vektors von  bei einer solchen Verschiebung
bei einer solchen Verschiebung
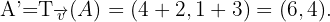
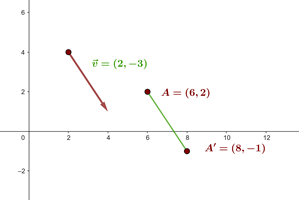
Eine Verschiebung in der Ebene ist durch den Vektor 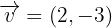 gegeben. Ermittle die Abbildung eines Punktes
gegeben. Ermittle die Abbildung eines Punktes 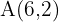 durch diese Verschiebung.
durch diese Verschiebung.
Wir denken daran, dass die Verschiebung um den Vektor 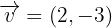 gegeben ist durch
gegeben ist durch
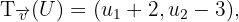
wobei 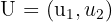 . Daher ist die Abbildung des Vektors von
. Daher ist die Abbildung des Vektors von 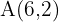 durch eine solche Verschiebung
durch eine solche Verschiebung
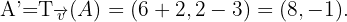
Die Abbildung durch Verschiebung eines Vektors  des Punkts
des Punkts  ist
ist 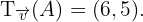 Ermittle den Verschiebungsvektor.
Ermittle den Verschiebungsvektor.
Wir denken daran, dass die Verschiebung um den Vektor 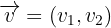 gegeben ist durch
gegeben ist durch
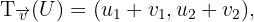
wobei 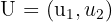 . Somit lautet die Abbildung dieser Verschiebung des Vektors
. Somit lautet die Abbildung dieser Verschiebung des Vektors 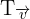 am Punkt
am Punkt 
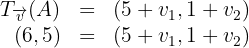
Wir setzen die Koordinaten gleich und erhalten
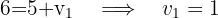
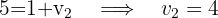
Die Abbildung durch Verschiebung eines Vektors  des Punktes
des Punktes 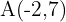 ist
ist 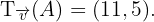 Ermittle den Verschiebungsvektor.
Ermittle den Verschiebungsvektor.
Wir denken daran, dass die Verschiebung um den Vektor 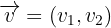 gegeben ist durch
gegeben ist durch
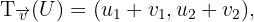
wobei 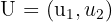 . Somit lautet die Abbildung durch diese Verschiebung des Vektors
. Somit lautet die Abbildung durch diese Verschiebung des Vektors 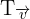 am Punkt
am Punkt 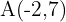
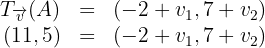
Wir setzen die Koordinaten gleich und erhalten
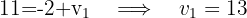

Die Abbildung durch Verschiebung eines Vektors  des Punktes
des Punktes 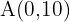 ist
ist 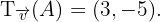 Ermittle den Verschiebungsvektor.
Ermittle den Verschiebungsvektor.
Wir denken daran, dass die Verschiebung um den Vektor 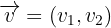 gegeben ist durch
gegeben ist durch
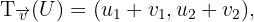
wobei 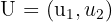 . Somit ist die Abbildung dieser Verschiebung des Vektors
. Somit ist die Abbildung dieser Verschiebung des Vektors 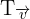 im Punkt
im Punkt 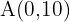 , es
, es
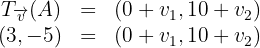
Wir setzen die Koordinaten gleich und erhalten
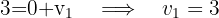

Verschiebung von Kreisen
Eine Verschiebung in der Ebene ist durch den Vektor 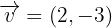 definiert.
definiert.
a Ermittle die Abbildung durch diese Verschiebung eines Punktes 
b Ermittle die Verschiebung eines Kreises mit dem Mittelpunkt  und dem Radius
und dem Radius 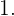
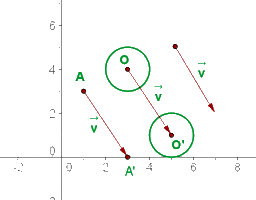
Um den Teil a zu lösen, können wir genauso vorgehen, wie in Aufgabe 1. In diesem Fall ist die durch 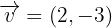 definierte Verschiebung
definierte Verschiebung
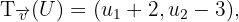
wobei 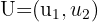 .
.
Daraus folgt, dass die Abbildung des Punktes 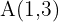 bei dieser Verschiebung wie folgt lautet
bei dieser Verschiebung wie folgt lautet
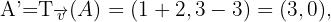
wie die Figur zeigt.
Um den Abschnittb zu lösen, müssen wir die Verschiebung des Mittelpunktes des Kreises um den Vektor 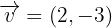 durchführen. Die gesuchte Verschiebung ist dann der Kreis mit dem Mittelpunkt in der Verschiebung und dem Radius 1, also dem gleichen Radius wie der ursprüngliche Kreis.
durchführen. Die gesuchte Verschiebung ist dann der Kreis mit dem Mittelpunkt in der Verschiebung und dem Radius 1, also dem gleichen Radius wie der ursprüngliche Kreis.
Wir erhalten die Verschiebung des Mittelpunktes:
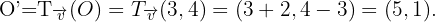
Wie bereits erwähnt, ist die Verschiebung des Kreises mit dem Mittelpunkt  und dem Radius
und dem Radius 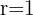 der Kreis mit dem Mittelpunkt
der Kreis mit dem Mittelpunkt 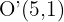 und dem Radius
und dem Radius 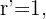 wie in der Abbildung dargestellt.
wie in der Abbildung dargestellt.
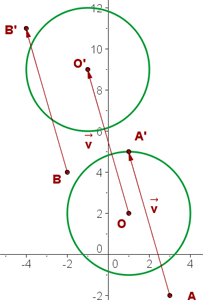
Bei einer Verschiebung mittels des Vektors  wird ein Punkt
wird ein Punkt 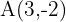 in einen Punkt
in einen Punkt 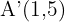 umgewandelt. Berechne:
umgewandelt. Berechne:
aDie Verschiebung des Punktes 
bDie Verschiebung eines Kreises mit Mittelpunkt 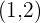 und Radius
und Radius 
Für den Abschnitt a ermitteln wir den 1. Vektor  . Dies können wir
. Dies können wir
wie folgt tun: Die Verschiebung um  des Punktes
des Punktes 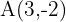 ist gleich
ist gleich 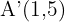 , somit
, somit

Diese Gleichung sagt uns, dass 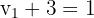 und
und  .
.
Wir ermitteln 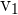 und
und 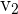 . Es gilt
. Es gilt 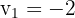 sowie
sowie  und somit
und somit  .
.
Schließlich ist die Verschiebung von  in Bezug auf
in Bezug auf 
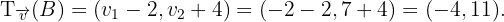
Wir stellen fest, dass wir dieses Ergebnis in der Abbildung sehen.
Um b zu lösen, müssen wir zunächst den Mittelpunkt  verschieben
verschieben

Die Verschiebung eines Kreises mit Mittelpunkt  und Radius
und Radius 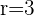 ist also ein Kreis mit Mittelpunkt
ist also ein Kreis mit Mittelpunkt 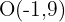 und Radius
und Radius 
Eine Verschiebung in der Ebene ist durch den Vektor 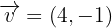 definiert. Ermittle die Verschiebung des Kreises
definiert. Ermittle die Verschiebung des Kreises 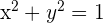
Zunächst stellen wir fest, dass der Mittelpunkt des Kreises 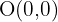 ist. Wir müssen die Verschiebung des Mittelpunkts finden:
ist. Wir müssen die Verschiebung des Mittelpunkts finden:
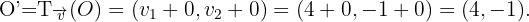
Somit ist die Verschiebung eines Kreises 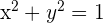 und dem Radius
und dem Radius 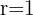 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt 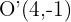 und dem Radius
und dem Radius 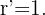
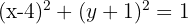
Eine Verschiebung in der Ebene ist durch den Vektor 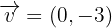 gegeben. Ermittle die Verschiebung des Kreises
gegeben. Ermittle die Verschiebung des Kreises 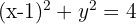
Zunächst sehen wir, dass der Mittelpunkt des Kreises 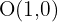 und der Radius
und der Radius  ist. Nun müssen wir die Verschiebung des Mittelpunktes ermitteln:
ist. Nun müssen wir die Verschiebung des Mittelpunktes ermitteln:
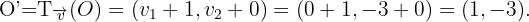
Somit ist die Verschiebung eines Kreises 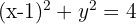 und dem Radius
und dem Radius  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt 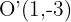 und dem Radius
und dem Radius 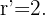
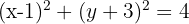
Eine Verschiebung in der Ebene ist durch einen Vektor 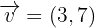 definiert. Ermittle die Verschiebung des Kreises
definiert. Ermittle die Verschiebung des Kreises 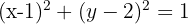
Zunächst stellen wir fest, dass der Mittelpunkt des Kreises  und der Radius
und der Radius 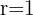 ist. Nun müssen wir die Verschiebung des Mittelpunktes ermitteln:
ist. Nun müssen wir die Verschiebung des Mittelpunktes ermitteln:
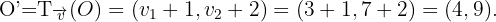
Somit ist die Verschiebung eines Kreises 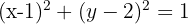 und dem Radius
und dem Radius 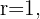 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt 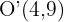 und dem Radius
und dem Radius 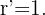
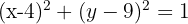
Verschiebung von Dreicken
Eine Verschiebung hat den Vektor 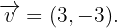 Ermittle die Verschiebung der Figur eines Dreiecks, dessen Eckpunkte wie folgt sind:
Ermittle die Verschiebung der Figur eines Dreiecks, dessen Eckpunkte wie folgt sind: 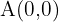 ,
, 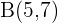 und
und 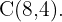
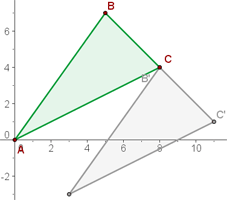
Die Verschiebung eines Dreiecks mit den Eckpunkten 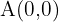 ,
, 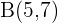 und
und  ist das Dreieck mit den Eckpunkten
ist das Dreieck mit den Eckpunkten  ,
,  und
und 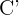 , wobei
, wobei  die Verschiebung von
die Verschiebung von  ,
,  die Verschiebung von
die Verschiebung von  und
und 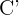 die Verschiebung von
die Verschiebung von  ist. Für alle Verschiebungen gilt der Vektor
ist. Für alle Verschiebungen gilt der Vektor 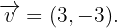
Wir können nun die Verschiebungen berechnen.
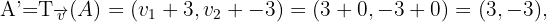
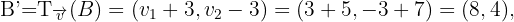
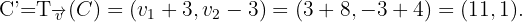
Wie wir in der Abbildung sehen können, sind die Eckpunkte des gesuchten Dreiecks 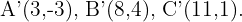 .
.
Eine Verschiebung hat den Vektor 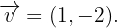 Ermittle die Verschiebung der Figur eines Dreiecks mit den Eckpunkten:
Ermittle die Verschiebung der Figur eines Dreiecks mit den Eckpunkten: 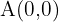 ,
, 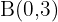 und
und 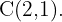
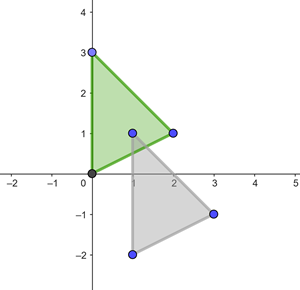
Die Verschiebung eines Dreiecks mit den Eckpunkten 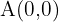 ,
, 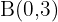 und
und 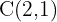 ist ein Dreieck mit den Eckpunkten
ist ein Dreieck mit den Eckpunkten  ,
,  und
und 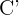 , wobei
, wobei  die Verschiebung von
die Verschiebung von  ,
,  die Verschiebung von
die Verschiebung von  und
und 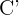 die Verschiebung von
die Verschiebung von  ist. Für alle Verschiebungen gilt der Vektor
ist. Für alle Verschiebungen gilt der Vektor 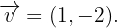
Wir können nun die Verschiebungen berechnen.
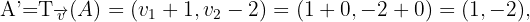
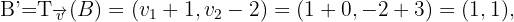
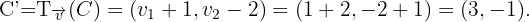
Wie wir in der Abbildung sehen können, hat das gesuchte Dreieck die Eckpunkte 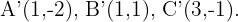
Die Abbildungen durch Verschiebung eines Vektors  der Eckpunkte
der Eckpunkte 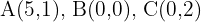 eines Dreiecks sind
eines Dreiecks sind 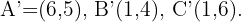 Ermittle den Verschiebungsvektor.
Ermittle den Verschiebungsvektor.
Die Verschiebung durch den Vektor 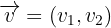 ist gegeben durch
ist gegeben durch
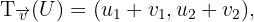
wobei 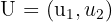 . Da die Verschiebung der Eckpunkte gleich ist, betrachten wir nur die Abbildung durch diese Verschiebung des Vektors
. Da die Verschiebung der Eckpunkte gleich ist, betrachten wir nur die Abbildung durch diese Verschiebung des Vektors 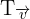 im Punkt
im Punkt 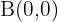 , es
, es
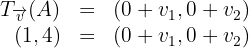
Wir setzen die Koordinaten gleich und erhalten
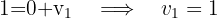
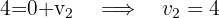
Ein Dreieck hat die Eckpunkte 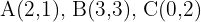 . Es wird eine Verschiebung durch den Vektor
. Es wird eine Verschiebung durch den Vektor 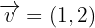 durchgeführt. Ermittle die verschobenen Eckpunkte.
durchgeführt. Ermittle die verschobenen Eckpunkte.
Wir berechnen die Verschiebungen.
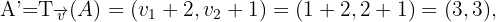
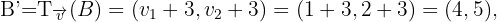
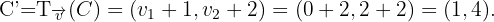
Somit hat das gesuchte Dreieck die Eckpunkte 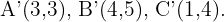
Ein Dreieck hat die Eckpunkte 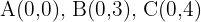 . Es wird eine Verschiebung durch den Vektor
. Es wird eine Verschiebung durch den Vektor 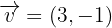 durchgeführt. Berechne die verschobenen Eckpunkte.
durchgeführt. Berechne die verschobenen Eckpunkte.
Wir berechnen die Verschiebungen.
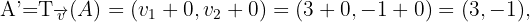
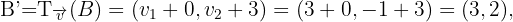
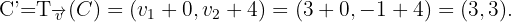
Somit hat das gesuchte Dreieck die Eckpunkte 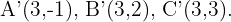
Mit KI zusammenfassen:













