Bei diesen Übungen wird davon ausgegangen, dass du bereits die Definition einer Ungleichung und einige ihrer Eigenschaften kennst. Sollte dies nicht der Fall sein, empfehlen wir dir, dass du dir unseren Artikel zur Theorie ansiehst.
Wir werden jede Aufgabe Schritt für Schritt lösen. Wir sollten beachten, dass das Lösen einer Ungleichung praktisch dasselbe ist wie das Lösen einer Gleichung, nur dass wir jetzt genau auf die Eigenschaften von Ungleichungen achten müssen, wann sie "ihren Sinn ändern", usw. Wir werden jeden Schritt algebraisch darstellen und dabei versuchen, so detailliert wie möglich zu sein.
Finde die Lösung für jede der folgenden Ungleichungen bzw. Ungleichungssysteme und stelle die Lösungsmenge grafisch dar.

Wir lösen nun die Ungleichung. Wir dürfen nicht vergessen, dass dies dem Lösen einer Gleichung sehr ähnlich ist, nur dass wir jetzt nicht mehr nur einen Wert für unsere Variable bestimmen, sondern einen ganzen Bereich, der oft aus einem Intervall oder aus Vereinigungen oder Überschneidungen von Intervallen besteht. Unsere Ungleichung ist:

Als Erstes wenden wir das Distributivgesetz an und bestimmen danach 
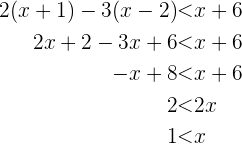
Dies sagt uns, dass  . Die Lösungsmenge ist also das Intervall
. Die Lösungsmenge ist also das Intervall  .
.


Wir lösen folgende Ungleichung:

Wir kümmern uns zunächst um die Brüche und bestimmen dann  . Um die Brüche loszuwerden benötigen wir das kleinste gemeinsame Vielfache der Nenner. Dies ist
. Um die Brüche loszuwerden benötigen wir das kleinste gemeinsame Vielfache der Nenner. Dies ist 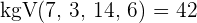 . Wir erhalten somit
. Wir erhalten somit

Dies sagt uns, dass  . Die Lösungsmenge ist also das Intervall
. Die Lösungsmenge ist also das Intervall  .
.

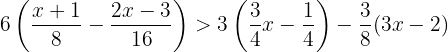
Wir lösen folgende Ungleichung:
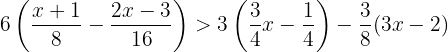
Wir gehen genauso vor, wie im vorherigen Beispiel. Wir wenden das Distributivgesetz an und eliminieren außerdem noch die Brüche

Dies sagt uns, dass  x < \frac{5}{3}[/latex]. Die Lösungsmenge ist also das Intervall [latex]\displaystyle \left( -\infty, \frac{5}{3}\right)[/latex].
x < \frac{5}{3}[/latex]. Die Lösungsmenge ist also das Intervall [latex]\displaystyle \left( -\infty, \frac{5}{3}\right)[/latex].
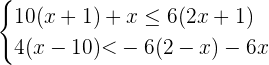
Um dieses System zu lösen, müssen wir die Ungleichungen einzeln lösen. Außerdem müssen wir die Werte bestimmen, für die  beide Gleichungen erfüllt.
beide Gleichungen erfüllt.
Wir beginnen mit der ersten Ungleichung

Aus der ersten Ungleichung erhalten wir  . Somit ist
. Somit ist  Teil des Intervalls
Teil des Intervalls  . Nun lösen wir die zweite Ungleichung
. Nun lösen wir die zweite Ungleichung
 . Somit ist
. Somit ist  Teil des Intervalls
Teil des Intervalls  . Wir stellen fest, dass x beide Bedingungen erfüllen muss, also
. Wir stellen fest, dass x beide Bedingungen erfüllen muss, also  und
und  . Man kann auch sagen, dass
. Man kann auch sagen, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehört. Die Lösungsmenge ist also
gehört. Die Lösungsmenge ist also




Wir lösen die Aufgabe
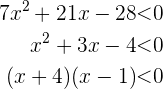
Dies sagt uns, dass  . Das Produkt ist jedoch nur dann negativ, wenn die zu multiplizierenden Ausdrücke unterschiedliche Vorzeichen haben. Dies bedeutet, dass es zwei Hauptfälle gibt:
. Das Produkt ist jedoch nur dann negativ, wenn die zu multiplizierenden Ausdrücke unterschiedliche Vorzeichen haben. Dies bedeutet, dass es zwei Hauptfälle gibt: 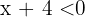 und
und 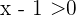 sowie
sowie 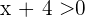 und
und  .
.
Wir sehen uns jeden der Fälle an. Wir nehmen an, dass 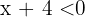 und somit
und somit  . Außerdem haben wir
. Außerdem haben wir 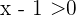 und somit
und somit 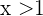 . Das heißt,
. Das heißt,  muss die Bedingungen
muss die Bedingungen  und
und 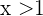 erfüllen und somit zur Schnittmenge der Intvervalle
erfüllen und somit zur Schnittmenge der Intvervalle  und
und  gehören. Wir stellen fest, dass die Schnittmenge leer ist; die besagten Intervalle schneiden sich nicht. Somit haben wir in diesem Fall keine Lösung.
gehören. Wir stellen fest, dass die Schnittmenge leer ist; die besagten Intervalle schneiden sich nicht. Somit haben wir in diesem Fall keine Lösung.
Nun sehen wir uns den zweiten Fall an. Wir nehmen an, dass 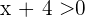 und somit
und somit 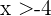 . Außerdem haben wir
. Außerdem haben wir  und somit
und somit  . Das heißt,
. Das heißt,  muss die Bedingungen
muss die Bedingungen 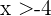 und
und  erfüllen und somit zur Schnittmenge der Intervalle
erfüllen und somit zur Schnittmenge der Intervalle  und
und  gehören. Die Schnittmenge ist
gehören. Die Schnittmenge ist  und dieses Intervall ist somit das gesuchte Intervall.
und dieses Intervall ist somit das gesuchte Intervall.


Wir lösen unsere Ungleichung

Wir beginnen mit dem Lösen der Aufgabe
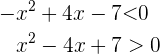
Um  als Produkt von Ausdrücken 1. Grades auszudrücken, müssen wir die Nullstellen bestimmen und wenden dafür die Mitternachtsformel an
als Produkt von Ausdrücken 1. Grades auszudrücken, müssen wir die Nullstellen bestimmen und wenden dafür die Mitternachtsformel an

Da unter der Wurzel jedoch eine negative Zahl steht, sind die Nullstellen des Polynoms komplexe Zahlen. Weil wir das Polynom also nicht als Ausdruck mit reellen Zahlen schreiben können, setzen wir zur Lösung für  eine reelle Zahl ein. Wenn die Ungleichung erfüllt ist, sind die reellen Zahlen
eine reelle Zahl ein. Wenn die Ungleichung erfüllt ist, sind die reellen Zahlen  die Lösungsmenge. Wenn die Ungleichung nicht erfüllt ist, gibt es keine Lösung. Wir setzen ein:
die Lösungsmenge. Wenn die Ungleichung nicht erfüllt ist, gibt es keine Lösung. Wir setzen ein: 
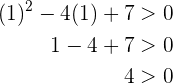
Da 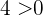 , ist die Lösungsmenge
, ist die Lösungsmenge  .
.

Die gegebene Ungleichung ist

Wir lösen
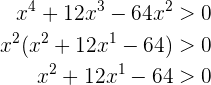
Am Ende wird durch  dividiert, denn da der Ausdruck positiv ist, ist es unmöglich, dass
dividiert, denn da der Ausdruck positiv ist, ist es unmöglich, dass  . Somit gilt
. Somit gilt  . Nun berechnen wir die Nullstellen von
. Nun berechnen wir die Nullstellen von  und schreiben unsere Ungleichung als
und schreiben unsere Ungleichung als
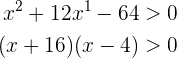
Wir haben 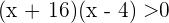 . Das Produkt ist jedoch nur dann positiv, wenn die zu multiplizierenden Ausdrücke das gleiche Vorzeichen haben. Dies bedeutet, dass es zwei Hauptfälle gibt:
. Das Produkt ist jedoch nur dann positiv, wenn die zu multiplizierenden Ausdrücke das gleiche Vorzeichen haben. Dies bedeutet, dass es zwei Hauptfälle gibt:  und
und  sowie
sowie 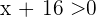 und
und 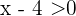 .
.
Wir sehen uns jeden der Fälle an und beginnen mit dem ersten Fall. Wir nehmen an, dass  und somit
und somit  sowie
sowie  und somit
und somit  . Für
. Für  muss also
muss also  und
und  gelten und es muss zur Schnittmenge der Intervalle
gelten und es muss zur Schnittmenge der Intervalle  und
und  gehören. Die Schnittmenge ist
gehören. Die Schnittmenge ist  und somit eine Lösung.
und somit eine Lösung.
Nun sehen wir uns den zweiten Fall an. Wir nehmen an, dass 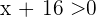 und somit
und somit 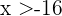 sowie
sowie 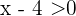 und somit
und somit 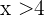 . Für
. Für  muss also
muss also 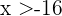 und
und 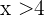 gelten und es muss zur Schnittmenge der Intervalle
gelten und es muss zur Schnittmenge der Intervalle  und
und  gehören. Die Schnittmenge ist
gehören. Die Schnittmenge ist  und das Intervall ist somit auch eine Lösung.
und das Intervall ist somit auch eine Lösung.
Unsere endgültige Lösung ist also die Vereinigung der beiden gefundenen Einzellösungen, also  .
.



Wir lösen
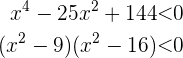
Dies sagt uns, dass  . Das Produkt ist jedoch nur dann negativ, wenn die zu multiplizierenden Ausdrücke unterschiedliche Vorzeichen haben. Wir haben also zwei Hauptfälle:
. Das Produkt ist jedoch nur dann negativ, wenn die zu multiplizierenden Ausdrücke unterschiedliche Vorzeichen haben. Wir haben also zwei Hauptfälle: 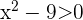 und
und  sowie
sowie  und
und 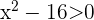 .
.
Wir sehen uns jeden der Fälle an und beginnen mit dem ersten Fall. Wir gehen davon aus, dass wir das Polynom 2. Grades  zunächst als Produkt von Ausdrücken vom Grad 1 ausdrücken müssen. Somit
zunächst als Produkt von Ausdrücken vom Grad 1 ausdrücken müssen. Somit
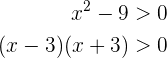
Damit dies positiv ist, müssen  und
und  dasselbe Vorzeichen haben, also beide positiv oder beide negativ sein. Wenn beide negativ sind, gilt für
dasselbe Vorzeichen haben, also beide positiv oder beide negativ sein. Wenn beide negativ sind, gilt für 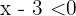 , dass
, dass  und für
und für  gilt, dass
gilt, dass  . Man kann auch sagen, dass
. Man kann auch sagen, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehört, die
gehört, die  ist.
ist.
Nun gehen wir davon aus, dass  und
und  positiv sind. Für
positiv sind. Für 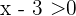 gilt
gilt 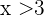 und für
und für 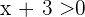 gilt
gilt 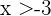 . Man kann auch sagen, dass
. Man kann auch sagen, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehört, die
gehört, die  ist.
ist.
Damit 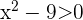 erfüllt ist, muss
erfüllt ist, muss  zur Vereinigung der zwei vorher ermittelten Intervalle gehören.
zur Vereinigung der zwei vorher ermittelten Intervalle gehören.  gehört also zu
gehört also zu  .
.
Da wir davon ausgehen, dass 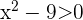 , folgt auch, dass
, folgt auch, dass  . Wir müssen dieses Polynom also als Produkt von Ausdrücken 1. Grades schreiben
. Wir müssen dieses Polynom also als Produkt von Ausdrücken 1. Grades schreiben
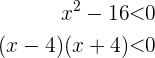
Damit dies negativ ist, müssen  und
und  unterschiedliche Vorzeichen haben. Wenn wir annehmen, dass
unterschiedliche Vorzeichen haben. Wenn wir annehmen, dass  und
und 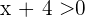 gilt jeweils
gilt jeweils  und
und 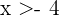 . Das bedeutet, dass
. Das bedeutet, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehört, die
gehört, die  ist.
ist.
Nun nehmen wir an, dass 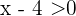 und
und 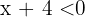 . Es muss also jeweils
. Es muss also jeweils 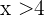 und
und  gelten. Das heißt, dass
gelten. Das heißt, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehört, die leer ist. Die einzige Möglichkeit, dass
gehört, die leer ist. Die einzige Möglichkeit, dass  ist, dass
ist, dass  zum Intervall
zum Intervall  gehört.
gehört.
All dies zeigt uns: Damit 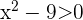 und
und  erfüllt ist, muss
erfüllt ist, muss  zur Schnittmenge der ermittelten Lösungsmengen
zur Schnittmenge der ermittelten Lösungsmengen  und
und  gehören, die
gehören, die  ist.
ist.
Wir fahren mit unserer zweiten ursprünglichen Annahme fort, nämlich  und
und 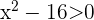 . Wir nehmen an, dass
. Wir nehmen an, dass  und müssen dieses Polynom 2. Grades in ein Produkt von Ausdrücken vom Grad 1 umwandeln
und müssen dieses Polynom 2. Grades in ein Produkt von Ausdrücken vom Grad 1 umwandeln
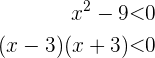
Damit dies negativ ist, müssen  und
und  unterschiedliche Vorzeichen haben. Für
unterschiedliche Vorzeichen haben. Für 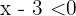 und
und 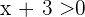 muss jeweils
muss jeweils  und
und 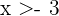 gelten. Das heißt, dass
gelten. Das heißt, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehören muss, die
gehören muss, die  ist.
ist.
Nun muss für 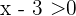 und
und  jeweils
jeweils 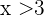 und
und  gelten. Das heißt, dass
gelten. Das heißt, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  ghören muss, die leer ist. Die einzige Möglichkeit für
ghören muss, die leer ist. Die einzige Möglichkeit für  ist, dass
ist, dass  zum Intervall
zum Intervall  gehört
gehört
Außerdem haben wir 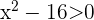 und müssen dieses Polynom vom Grad 2 in ein Produkt von Ausdrücken vom Grad 1 umwandeln
und müssen dieses Polynom vom Grad 2 in ein Produkt von Ausdrücken vom Grad 1 umwandeln
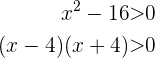
Damit dies positiv ist, müssen  und
und  das gleiche Vorzeichen haben. Beide müssen also positiv oder negativ sein. Wenn beide negativ sind, muss für
das gleiche Vorzeichen haben. Beide müssen also positiv oder negativ sein. Wenn beide negativ sind, muss für  gelten, dass
gelten, dass  . Für
. Für 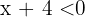 muss gelten, dass
muss gelten, dass  . Das heißt, dass
. Das heißt, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehören muss, die
gehören muss, die  ist.
ist.
Nun nehmen wir an, dass  und
und  positiv sind. Für
positiv sind. Für 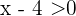 muss gelten, dass
muss gelten, dass 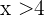 und für
und für 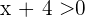 muss gelten, dass
muss gelten, dass 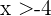 . Das heißt, dass
. Das heißt, dass  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehören muss, die
gehören muss, die  ist.
ist.
Damit also 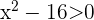 erfüllt ist, muss
erfüllt ist, muss  zur Vereinigung der beiden vorher ermittelten Intervalle gehören. Also gehört
zur Vereinigung der beiden vorher ermittelten Intervalle gehören. Also gehört  zu
zu  .
.
Und damit 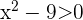 und
und 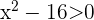 erfüllt sind, muss
erfüllt sind, muss  zur Schnittmenge der vorher ermittelten Lösungsmengen
zur Schnittmenge der vorher ermittelten Lösungsmengen  und
und  gehören, die leer ist.
gehören, die leer ist.
Unsere endgültige Lösung wäre die Vereinigung der beiden Lösungen für jeden Fall. Da die letzte Lösung jedoch leer ist, ist die endgültige Lösungsmenge  .
.


Wir lösen folgende Ungleichung:

Wir formen um

Damit der Bruch gleich null ist, muss der Zähler null sein. Also  und somit
und somit  .
.
Damit der Bruch negativ ist, müssen der Zähler und der Nenner unterschiedliche Vorzeichen haben. Zunächst nehmen wir an, dass der Zähler positiv ist und der Nenner negativ. Für 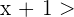 bedeutet das
bedeutet das 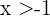 und für
und für  bedeutet das
bedeutet das  . Also muss
. Also muss  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehören, die
gehören, die  ist.
ist.
Nun nehmen wir an, dass der Zähler negativ ist und der Nenner positiv. Für 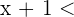 bedeutet das
bedeutet das  und für
und für 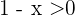 bedeutet das
bedeutet das 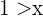 . Also muss
. Also muss  zur Schnittmenge der Intervalle
zur Schnittmenge der Intervalle  und
und  gehören, die
gehören, die  ist.
ist.
Aus all dem können wir ableiten, dass, damit  erfüllt ist,
erfüllt ist,  zur Vereinigung der beiden ermittelten Intervalle und dem Punkt
zur Vereinigung der beiden ermittelten Intervalle und dem Punkt  gehören muss. Die Lösungsmenge ist also
gehören muss. Die Lösungsmenge ist also 




