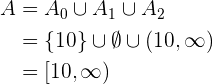Eine gebrochene Ungleichung ist eine Ungleichung, bei der die Unbekannte sowohl im Nenner als auch im Zähler steht. Im Allgemeinen haben die gebrochenen Ungleichungen eine der folgenden Formen
1 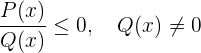
2 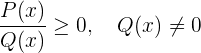
3 
4 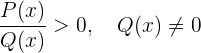
Du erfährst in den ersten beiden Fällen, wie du vorgehen musst. Die Schritte sind einfach: Du musst die Werte von  im Zähler und im Nenner finden, für die die Ungleichung erfüllt ist, wobei du in der Regel Schnittpunkte und Vereinigungen der Intervalle verwendest.
im Zähler und im Nenner finden, für die die Ungleichung erfüllt ist, wobei du in der Regel Schnittpunkte und Vereinigungen der Intervalle verwendest.
Erster wichtiger Fall
Beginne mit 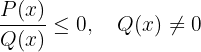 .
.
1 Zunächst musst du die Werte finden, für die 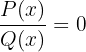 ist. Dazu findest du die Werte von
ist. Dazu findest du die Werte von  für die der Zähler gleich Null ist, d. h. du löst
für die der Zähler gleich Null ist, d. h. du löst 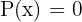 . Bezeichne die Menge der Werte, für die
. Bezeichne die Menge der Werte, für die 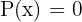 als
als  .
.
2 Du weißt, dass 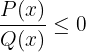 ist, da du bereits die Werte gefunden hast, konzentriere dich jetzt nur auf
ist, da du bereits die Werte gefunden hast, konzentriere dich jetzt nur auf 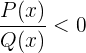 .
.
Es gibt zwei Fälle, in denen 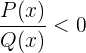 ist. Das ist immer dann der Fall, wenn die Nenner
ist. Das ist immer dann der Fall, wenn die Nenner  und
und  entgegengesetzte Vorzeichen haben.
entgegengesetzte Vorzeichen haben.
Dein erster Fall ist also 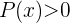 und
und 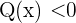 . Die Menge der Werte, für die
. Die Menge der Werte, für die 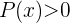 ist
ist  , und die Menge der Werte, für die
, und die Menge der Werte, für die 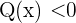 als
als  , dann ist die Lösungsmenge, für die beide Ungleichungen
, dann ist die Lösungsmenge, für die beide Ungleichungen 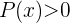 und
und 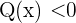 erfüllt sind, die Schnittmenge
erfüllt sind, die Schnittmenge  . Beachte, dass du
. Beachte, dass du 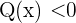 und nicht
und nicht  verwendest, da
verwendest, da  der Nenner ist und nicht gleich Null sein kann.
der Nenner ist und nicht gleich Null sein kann.
Dein zweiter Fall ist 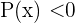 und
und 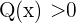 . Die Menge der Werte, für die
. Die Menge der Werte, für die 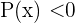 ist
ist  , und die Menge der Werte, für die
, und die Menge der Werte, für die 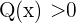 als
als  , dann ist die Lösungsmenge, für die beide Ungleichungen
, dann ist die Lösungsmenge, für die beide Ungleichungen 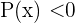 und
und 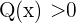 erfüllt sind, die Schnittmenge
erfüllt sind, die Schnittmenge  . Beachte, dass du
. Beachte, dass du 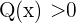 und nicht
und nicht 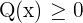 nimmst, da
nimmst, da  der Nenner ist und nicht gleich Null sein kann.
der Nenner ist und nicht gleich Null sein kann.
3 Die Lösungsmenge ist die Vereinigung der Mengen  ,
, 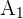 und
und 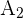 , d.h.
, d.h.

Für den Fall 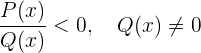 ist es ähnlich, konzentriere dich aber nur auf den zweiten und dritten Punkt.
ist es ähnlich, konzentriere dich aber nur auf den zweiten und dritten Punkt.
Zweiter wichtiger Fall
Betrachte nun den Fall, dass 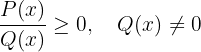
1 Zunächst musst du die Werte finden, für die 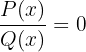 ist. Dazu findest du die Werte von
ist. Dazu findest du die Werte von  für die der Zähler gleich Null ist, d. h. du löst
für die der Zähler gleich Null ist, d. h. du löst 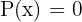 . Bezeichne die Menge der Werte, für die
. Bezeichne die Menge der Werte, für die 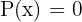 ist, als
ist, als  .
.
2 Du weißt, dass 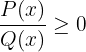 , da du bereits die Werte gefunden hast, wenn sie gleich Null ist, konzentriere dich jetzt nur auf
, da du bereits die Werte gefunden hast, wenn sie gleich Null ist, konzentriere dich jetzt nur auf 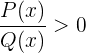 .
.
Es gibt zwei Fälle, in denen 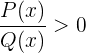 , ist. Dies ist immer dann der Fall, wenn der Nenner
, ist. Dies ist immer dann der Fall, wenn der Nenner  und
und  gleiche Vorzeichen haben.
gleiche Vorzeichen haben.
Dein erster Fall ist also 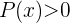 und
und 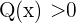 . Die Menge der Werte, für die
. Die Menge der Werte, für die 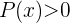 ist
ist  , und die Menge der Werte, für die
, und die Menge der Werte, für die 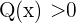 ist
ist  , dann ist die Lösungsmenge, für die beide Ungleichungen
, dann ist die Lösungsmenge, für die beide Ungleichungen 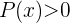 y
y 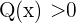 erfüllt sind, die Schnittmenge
erfüllt sind, die Schnittmenge  . Beachte, dass du
. Beachte, dass du 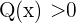 und nicht
und nicht 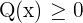 nimmst, da
nimmst, da  der Nenner ist und nicht gleich Null sein kann.
der Nenner ist und nicht gleich Null sein kann.
Dein zweiter Fall ist 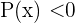 und
und 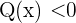 . Die Menge der Werte, für die
. Die Menge der Werte, für die 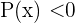 ist
ist  , und die Menge der Werte, für die
, und die Menge der Werte, für die 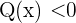 als
als  , dann ist die Lösungsmenge, für die beide Ungleichungen
, dann ist die Lösungsmenge, für die beide Ungleichungen 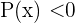 und
und 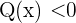 erfüllt sind, die Schnittmenge
erfüllt sind, die Schnittmenge  . Beachte, dass du
. Beachte, dass du 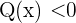 und nicht
und nicht  verwendest, da
verwendest, da  der Nenner ist und nicht gleich Null sein kann.
der Nenner ist und nicht gleich Null sein kann.
3 Die Lösungsmenge ist die Vereinigung der Mengen  ,
, 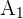 und
und 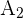 , d.h.
, d.h.

Für den Fall 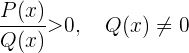 ist es ähnlich, konzentriere dich aber nur auf den zweiten und dritten Punkt.
ist es ähnlich, konzentriere dich aber nur auf den zweiten und dritten Punkt.
Beispiele
Normalerweise handelt es sich bei diesen Übungen  und
und  um Monome oder Produkte von Monomen. Anhand der folgenden Beispiele kannst du dir ein genaues Bild von dem Verfahren machen:
um Monome oder Produkte von Monomen. Anhand der folgenden Beispiele kannst du dir ein genaues Bild von dem Verfahren machen:
Löse die unten stehende Gleichung:

In diesem Fall ist  und
und 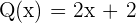 .
.
Beginne mit der Analyse, wann

Dazu musst du herausfinden, wann 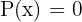 , oder
, oder 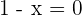 , ist, was eindeutig bei
, ist, was eindeutig bei  . der Fall ist. Deine erste Menge ist also
. der Fall ist. Deine erste Menge ist also 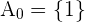 . Analysiere nun, wann
. Analysiere nun, wann
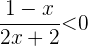
Du weißt bereits, dass es dafür zwei Fälle gibt, nämlich wenn der Nenner und der Zähler entgegengesetzte Vorzeichen haben. Beginne mit dem ersten Fall
1 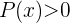 und
und 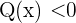 .
.
Du weißt bereits, dass dies gleichbedeutend ist mit 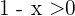 und
und 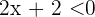 . Aus der ersten Ungleichung ergibt sich
. Aus der ersten Ungleichung ergibt sich
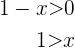
daraus folgt, dass die Lösungsmenge dieser Ungleichung 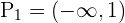 ist. Aus der zweiten ergibt sich
ist. Aus der zweiten ergibt sich
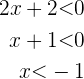
daraus folgt, dass die Lösungsmenge dieser Ungleichung 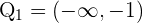 ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
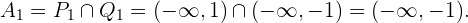
2 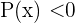 und
und 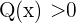 .
.
Du weißt bereits, dass dies gleichbedeutend ist mit  und
und 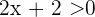 . Aus der ersten Ungleichung ergibt sich
. Aus der ersten Ungleichung ergibt sich
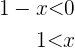
daraus folgt, dass die Lösungsmenge dieser Ungleichung 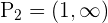 ist. Aus der zweiten ergibt sich
ist. Aus der zweiten ergibt sich
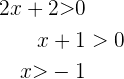
daraus folgt, dass die Lösungsmenge dieser Ungleichung  ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
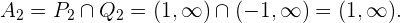
Schließlich ergibt sich, dass die allgemeine Lösung unserer Ungleichung die Vereinigung unserer drei Lösungen  ,
, 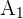 und
und 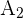 ist, d. h.
ist, d. h.
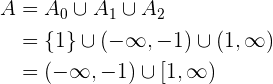
Löse die unten stehende Ungleichung

In diesem Fall ist 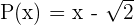 und
und 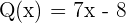 . Da sie hier strikt größer ist, ist es dir egal, wann der Bruch gleich Null ist, so dass du direkt zur Analyse der Ungleichung übergehst. Dabei gibt es zwei Fälle, nämlich wenn die Ziffern und der Nenner das gleiche Vorzeichen haben. Beginne mit dem ersten Fall
. Da sie hier strikt größer ist, ist es dir egal, wann der Bruch gleich Null ist, so dass du direkt zur Analyse der Ungleichung übergehst. Dabei gibt es zwei Fälle, nämlich wenn die Ziffern und der Nenner das gleiche Vorzeichen haben. Beginne mit dem ersten Fall
1 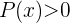 und
und 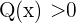 .
.
Du weißt bereits, dass dies gleichbedeutend ist mit 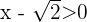 und
und 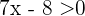 . Aus der ersten Ungleichung ergibt sich
. Aus der ersten Ungleichung ergibt sich
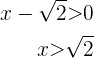
daraus folgt, dass die Lösungsmenge dieser Ungleichung 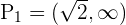 ist. Aus der zweiten ergibt sich
ist. Aus der zweiten ergibt sich
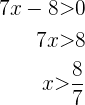
daraus folgt, dass die Lösungsmenge dieser Ungleichung 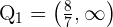 ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
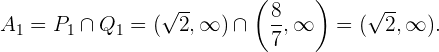
2 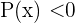 und
und 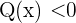 .
.
Du weißt bereits, dass dies gleichbedeutend ist mit 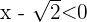 und
und 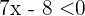 . Aus der ersten Ungleichung ergibt sich
. Aus der ersten Ungleichung ergibt sich
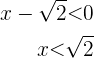
daraus folgt, dass die Lösungsmenge dieser Ungleichung 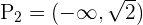 ist. Aus der zweiten ergibt sich
ist. Aus der zweiten ergibt sich
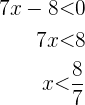
daraus folgt, dass die Lösungsmenge dieser Ungleichung 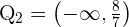 ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
ist. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
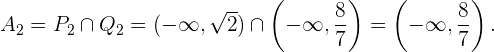
Schließlich ergibt sich, dass die allgemeine Lösung unserer Ungleichung die Vereinigung der beiden Lösungen 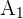 und
und 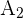 ist, d. h.
ist, d. h.
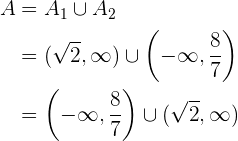
Löse die unten stehende Ungleichung:

In diesem Fall ist 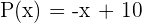 und
und 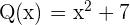 .
.
Beginne mit der Analyse, wann
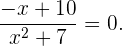
Dazu musst du herausfinden, wann 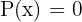 oder
oder 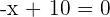 ist, was eindeutig bei
ist, was eindeutig bei 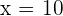 der Fall ist. Deine erste Menge ist also
der Fall ist. Deine erste Menge ist also 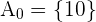 . Analysiere nun, wann
. Analysiere nun, wann
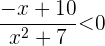
Du weißt bereits, dass es dafür zwei Fälle gibt, nämlich wenn Zähler und Nenner entgegengesetzte Vorzeichen haben. Beginne mit dem ersten Fall
1 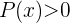 y
y 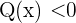 .
.
Beachte, dass verlangt wird, dass 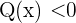 , was gleichbedeutend ist mit
, was gleichbedeutend ist mit
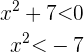
Allerdings ist 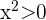 für alle
für alle 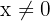 , so dass die obige Frage lautet
, so dass die obige Frage lautet
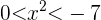
was zu 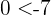 , führt, was niemals passieren kann. Daraus ergibt sich, dass die Bedingung
, führt, was niemals passieren kann. Daraus ergibt sich, dass die Bedingung 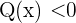 in diesem Fall nicht erfüllt sein kann,
in diesem Fall nicht erfüllt sein kann,
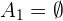
2 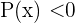 y
y 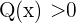 .
.
Du weißt bereits, dass dies gleichbedeutend ist mit 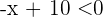 und
und 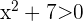 . Aus der ersten Ungleichung ergibt sich
. Aus der ersten Ungleichung ergibt sich
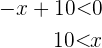
daraus folgt, dass die Lösungsmenge dieser Ungleichung 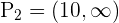 ist. Aus der zweiten ergibt sich, dass
ist. Aus der zweiten ergibt sich, dass 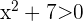 für alle
für alle  erfüllt ist, woraus folgt, dass die Lösungsmenge dieser Ungleichung
erfüllt ist, woraus folgt, dass die Lösungsmenge dieser Ungleichung 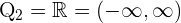 . Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
. Die Lösungsmenge für diesen Fall ist also die Schnittmenge, die lautet
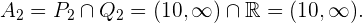
Schließlich ergibt sich, dass die allgemeine Lösung unserer Ungleichung die Vereinigung unserer drei Lösungen  ,
, 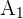 und
und 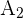 , ist, d. h.
, ist, d. h.