Kapitel
Die Definition des Skalarprodukts scheint auf den ersten Blick schwer zu verstehen, da sie häufig komplexe mathematische Gleichungen beinhaltet, aber dennoch ist es wichtig, sie zu kennen, um Konzepte der Physik verstehen zu können. Zum Beispiel findet es bei der Untersuchung von Randbedingungen in der Atmosphäre Anwendung, wie der Untersuchung von tief hängenden Wolken oder Regenschauern. Dort erleichtert die Einbeziehung des Skalarprodukts die Lösung von Rechenaufgaben.
Ein Skalarprodukt ist eine Skalar- oder Vektorgröße, die einen positiv definiten Wert hat, der größer oder gleich Null sein kann. Mit anderen Worten stellt das Skalarprodukt die Änderung einer messbaren Größe dar, z.B. eines Vektors, nicht aber unbedingt die tatsächliche Position oder Richtung, in die der Vektor zeigt. Die Skalarprodukte aus zwei oder mehr Vektoren sind in der Regel als die Summe aller entsprechenden Vektorgrößen definiert.
Das Skalarprodukt aus zwei Vektoren zu bilden, ist ein Rechenvorgang, bei dem eine reelle Zahl erzeugt wird:
Das Skalarprodukt wird in der Regel als Punkt 
notiert. Ebenfalls ist die Darstellung als 
bekannt. Bei Superprof verwenden wir immer die Schreibweise des Skalarprodukts anhand eines Punktes.
Das Skalarprodukt darf nicht mit der Multiplikation eines Vektors mit einem Skalar verwechselt werden.
Berechnungsarten des Skalarprodukts
Es gibt mehrere Möglichkeiten, um das Skalarprodukt aus zwei Vektoren 
und 
zu berechnen. Diese zeigen wir dir im Folgenden:
1 Wenn das Modul beider Vektoren sowie der Winkel 
, der zwischen ihnen liegt, feststehen, berechnet sich das Skalarprodukt wie folgt:
2 Wenn die Komponenten der Vektoren 
und 
feststehen, berechnet sich das Skalarprodukt wie folgt:
Beispiele
1 Gegeben seien die Vektoren 
und 
. Der Winkel zwischen den Vektoren beträgt 
.
Um das Skalarprodukt berechnen zu können, müssen wir zuerst das Modul von und ermitteln:
Das Skalarprodukt erhält man dann wie folgt:
2 Wir wiederholen den vorhergehenden Rechenprozess mit und . Dieses mal verwenden wir die Formel
Man sieht, dass man mit beiden Formeln dasselbe Ergebnis erhält.
Berechnung des Moduls und des Winkels zwischen Vektoren
Wie wir bereits gesehen haben, kann das Skalarprodukt auf zwei Arten berechnet werden. Es kann verwendet werden, um das Modul eines Vekors oder den Winkel zwischen zwei Vektoren zu berechnen.
Wie berechnet man das Modul eines Vektors mithilfe des Skalarprodukts?
Gegeben sei der Vektor :
Das heißt,
Mit dieser Formel kann das Modul des Vektors ermittelt werden, indem man das Skalarprodukt von mit dem Vektor selbst berechnet.
Wie berechnet man den Winkel zwischen zwei Vektoren mithilfe des Skalarprodukts?
Gegeben seien die Vektoren und .
Löse nach 
auf und du erhältst
Setze den Wert in die andere Formel für das Skalarprodukt ein und du erhältst
Mit dieser Formel kann der Winkel zwischen zwei Vektoren mithilfe der Arcus-Cosinus-Funktion berechnet werden.
Beispiele
1 Gegeben seien die Vektoren und . Das Modul dieser Vektoren ist:
2 Nun berechnen wir den Winkel zwischen und . Wir erhalten
Folglich ist
Wir erhalten
Orthogonalität zweier Vektoren
Zwei Vektoren sind orthogonal, wenn der Winkel zwischen ihnen 
oder 
beträgt. In beiden Fällen erhalten wir 
. Wenn zwei Vektoren orthogonal sind, gilt also:
Das heißt, zwei Vektoren 
und 
sind immer dann orthogonal, wenn folgendes erfüllt ist:
Beispiel
Ermittle, ob die Vektoren und aus den vorherigen Rechenbeispielen orthogonal sind. Man kann erkennen, dass
Folglich sind die Vektoren und nicht orthogonal.
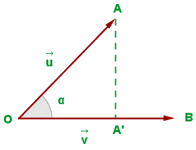
Geometrische Veranschaulichung des Skalarprodukts
Wie du auf der Grafik sehen kannst, kann 
als Länge der Abbildung des Vektors auf gesehen werden (solange 
ist). Die Abbildung wäre ein Vektor mit Ursprungspunkt 
und Endpunkt 
.
Wie wir wissen, ist
Daher erhalten wir beim Auflösen nach 
Um die Abbildung visualisieren zu können, stelle dir vor, dass es eine Lichtquelle gibt und die Abbildung der Schatten des Vektors auf dem Vektor ist. Die Lichtquelle muss außerdem so aufgestellt werden, dass ein zu orthogonaler Vektor keinen Schatten wirft.
Das Produkt 
ist also als Modul einer der Vektoren multipliziert mit dem Modul der Abbildung des anderen Vektors. Durch Einsetzen von 
in die Formel für das Skalarprodukt erhalten wir also
Wir berechnen das Modul der Abbildung des Vektors auf dem Vektor wie folgt:
Bemerke: Wenn negativ ist, bedeutet das, dass die Abbildung entgegen der Richtung des Vektors verläuft. Das ist der Fall, wenn 
oder 
ist. In diesem Fall ist das Modul der Abbildung durch 
gegeben.
Beispiel
Wir wollen die Abbildung des Vektors 
auf dem Vektor 
bilden. Dafür berechnen wir
hat ein negatives Vorzeichen. Daher verläuft die Abbildung in die entgegengesetzte Richtung zu und sein Modul ist 
.
Eigenschaften des Skalarprodukts
Das Skalarprodukt weist eine Vielzahl von Eigenschaften auf. Die wichtigsten sind die folgenden:
1 Das Skalarprodukt folgt dem Kommutativgesetz. In anderen Worten: die Reihenfolge der Faktoren hat keinen Einfluss auf das Produkt. Es spielt also keine Rolle, in welcher Reihenfolge die Vektoren miteinander multipliziert werden.
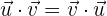
2 Die Multiplikation mit einem Skalar folgt dem Assoziativgesetz. Wenn wir mit multiplizieren und dann mit einem Skalar 
, erhalten wir dasselbe Ergebnis wie wenn wir zuerst 
berechnen und dann das Skalarprodukt mit bilden. Das heißt,
3 Das Skalarprodukt folgt dem Distributivgesetz in Bezug auf die Summe. Das heißt,
Bemerke: Die Eigenschaften 2 und 3 zusammen werden als Linearität des Skalarprodukts in Bezug auf die erste Variable bezeichnet.
Nota: Da das Skalarprodukt auch dem Kommutativgesetz folgt, gilt, dass es auch linear in Bezug auf die zweite Variable ist. Das heißt,
4 Das Skalarprodukt ist positiv definit. Das heißt, das Skalarprodukt eines Vektors, der ungleich Null ist, mit sich selbst ist immer positiv.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
