Definition und Eigenschaften
Eine Linearkombination von zwei oder mehr Vektoren ist der Vektor, den man erhält, wenn man einen Vektor mit einem Skalar multipliziert und dann mit einem anderen Vektor addiert. Eine Linearkombination ist also ein Ausdruck der Form:
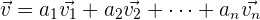
Für den besonderen Fall von zwei Vektoren 
, 
und zwei Zahlen 
, ist eine Linearkombination von und durch den Vektor 
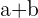gegeben .
Die folgende Abbildung zeigt die grafische Darstellung des Vektors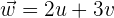 
.
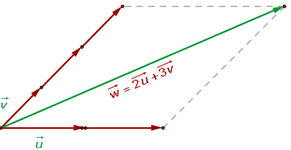
Beachte: Jeder Vektor in der Ebene kann als Linearkombination zweier anderer Vektoren mit unterschiedlichen Richtungen dargestellt werden. Außerdem ist diese Linearkombination eindeutig.
Beispiele zu Linearkombinationen
1 Gegeben sind die Vektoren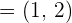 
und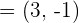 
. Bestimme die Linearkombination 
.
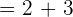Lösung: Um den Vektor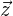 
zu bestimmen, müssen wir wie folgt vorgehen:
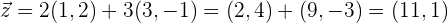
Somit
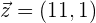
2 Drücke den Vektor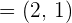 
als Linearkombination der Vektoren 
und 
aus.
Lösung: Wir nehmen an, dass 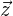als eine Linearkombination von 
und 
geschrieben werden kann. Das heißt, es gibt Konstanten 
und somit gilt 
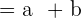. Wir müssen also nur die Konstanten bestimmen:
Somit
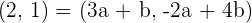
Wir müssen also das folgende lineare Gleichungssystem nach den Konstanten auflösen:
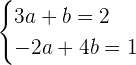
Dessen Lösung ist gegeben durch
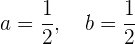
Somit können wir 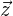wie folgt schreiben
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
