Kapitel
Formel zur Ableitung einer Logarithmusfunktion
Wenn wir eine Logarithmusfunktion
haben,
wenden wir die folgende Formel an, um sie abzuleiten:
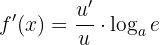
Oder anders gesehen, wie
Die oben beschriebene Formel entspricht also:
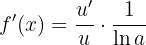
Ableitung mit natürlichem Logarithmus
Wenn wir eine Funktion mit natürlichem Logarithmus
haben,
lautet die Ableitung
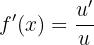
Aufgaben zur Ableitung der Logarithmusfunktion
Wir identifizieren 
und leiten ab
Wir wenden die Formel für die Ableitung von Logarithmusfunktionen an
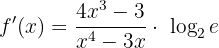
Um abzuleiten, müssen wir 
als Zusammensetzung zweier ableitbarer Funktionen darstellen
Somit
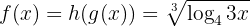
Wir leiten 
und 
ab und wenden hierfür die Formel zur Ableitung von Logarithmusfunktionen an
Wir wenden die Kettenregel an und berechnen
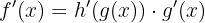
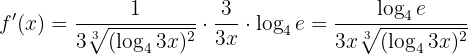
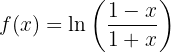
Unter Anwendung der Eigenschaften von Logarithmen erhalten wir
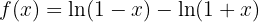
Wir leiten ab und berechnen
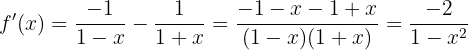
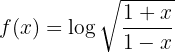
Unter Anwendung der Eigenschaften von Logarithmen erhalten wir
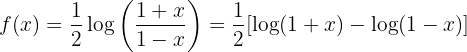
Wir leiten ab und berechnen
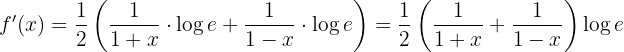
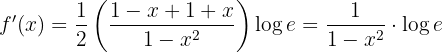
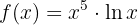
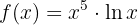
Wir stellen fest, dass die Funktion ein Produkt aus Funktionen ist
Wir leiten unter Berücksichtigung der Formel zur Ableitung von Logarithmusfunktionen ab
Wir wenden die Produktregel an
Wir setzen ein und berechnen
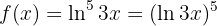
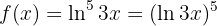
Um abzuleiten, müssen wir als Zusammensetzung zweier ableitbarer Funktionen darstellen
Somit
Wir leiten und unter Berücksichtigung der Formel zur Ableitung von Logarithmusfunktionen ab
Wir wenden die Kettenregel an und berechnen
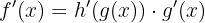
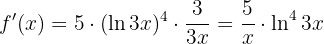
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
