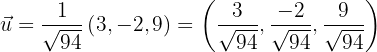Sei 
ein Vektor ungleich 0, dann hat dieser Vektor eine bestimmte Größe, Richtung und Orientierung. Um die Berechnungen zu vereinfachen, ist es oft notwendig, einen anderen Vektor zu generieren, der dieselbe Richtung und dieselbe Orientierung wie 
hat, aber eine Länge von eins aufweist. Aus diesem Grund wenden wir ein Verfahren an, das als Normierung bezeichnet wird.
Einen Vektor normieren
Normierung bedeutet, einen Vektor ungleich 0 zu nehmen und damit einen Vektor 
zu erhalten, der dieselbe Richtung und dieselbe Orientierung wie , aber die Länge 1 hat.
- Zunächst nehmen wir einen Vektor
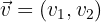ungleich 0 - Nun berechnen wir seine Länge (die ungleich 0 sein muss)
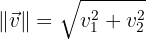
- Wir multiplizieren
mit dem Kehrwert der Länge und erhalten den Vektor 
Wir überprüfen also, ob die Länge von 1 ist.
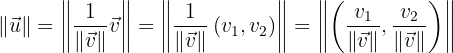
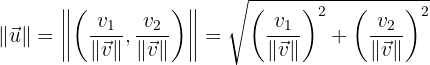
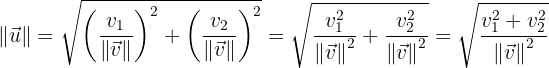
Dies bestätigt, dass der erhaltene Vektor die gewünschten Eigenschaften aufweist.
Beispielaufgaben zur Normierung
1 Wenn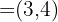 
, ermittle einen Einheitsvektor derselben Richtung und Orientierung.
Lösung:
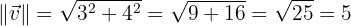
somit
Es ist wichtig zu erwähnen, dass der Vorgang auch für Dimensionen 
gültig ist, wie im folgenden Beispiel erläutert wird.
2 Wenn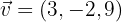 
, ermittle einen Einheitsvektor derselben Richtung und Orientierung.
Lösung:
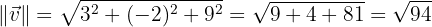
somit
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
