Löse die folgenden Probleme
1
Berechne die zentrische Streckung mit dem Zentrum im Ursprung und dem Verhältnis 
des folgenden Dreiecks, dessen Eckpunkte 
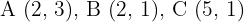sind.
, 
Dieses Feld ist erforderlich.
Da das Streckungsverhältnis ist, genügt es, die Koordinaten jedes Eckpunktes mit zu multiplizieren.
.
,
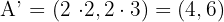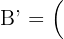Dieses Feld ist erforderlich.
.
,
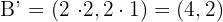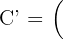Dieses Feld ist erforderlich.
.
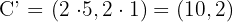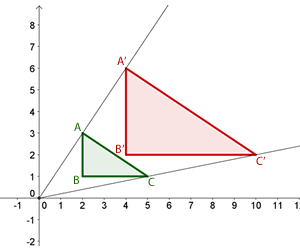
2
Ermittle die zentrische Streckung mit dem Zentrum im Ursprung und dem Verhältnis 
des Dreiecks mit den Eckpunkten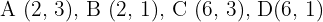 
.
,
Dieses Feld ist erforderlich.
Da das Streckungsverhältnis ist, genügt es, die Koordinaten jedes Eckpunktes mit zu multiplizieren.
.
,
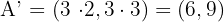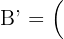Dieses Feld ist erforderlich.
.
,
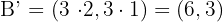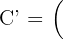Dieses Feld ist erforderlich.
.
,
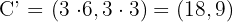Dieses Feld ist erforderlich.
.
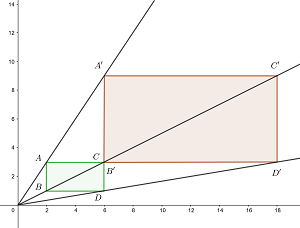
3
Gegeben ist ein Stern mit den Eckpunkten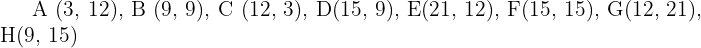 
.
Berechne die Fläche der zentrischen Streckung mit dem Zentrum im Ursprung und dem Verhältnis .
,
Dieses Feld ist erforderlich.
Da das Streckungsverhältnis ist, genügt es, die Koordinaten jedes Eckpunktes mit zu multiplizieren.
.
,
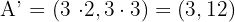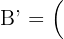Dieses Feld ist erforderlich.
.
,
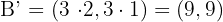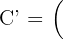Dieses Feld ist erforderlich.
.
,
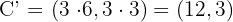Dieses Feld ist erforderlich.
.
,
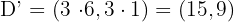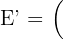Dieses Feld ist erforderlich.
.
,
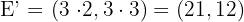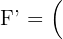Dieses Feld ist erforderlich.
.
,
Dieses Feld ist erforderlich.
.
,
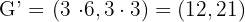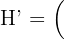Dieses Feld ist erforderlich.
.
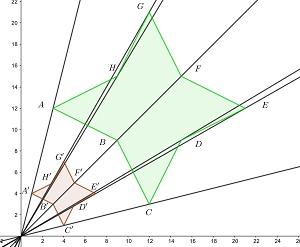
4
Gegeben ist ein Dreieck mit den Eckpunkten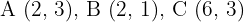 
. Berechne den Umfang der zentrischen Streckung mit dem Zentrum im Ursprung und dem Verhältnis 
.
Dieses Feld ist erforderlich.
Da das Streckungsverhältnis ist, genügt es, die Koordinaten jedes Eckpunktes mit zu multiplizieren.
.
.
.
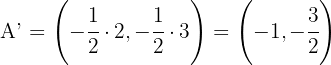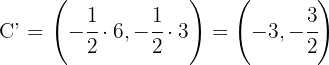Wir berechnen die Seiten des gestreckten Dreiecks
.
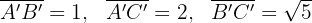Der Umfang ist
.
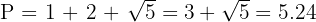Beachte, dass der Umfang der zentrischen Streckung gleich dem Umfang der ursprünglichen Figur multipliziert mit dem Betrag des gegebenen Verhältnisses ist
.
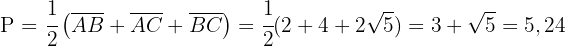5
Der Umfang eines Vielecks beträgt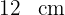 
. Berechne den Umfang 
der zentrischen Streckung mit dem Zentrum 
und dem Verhältnis .
Dieses Feld ist erforderlich.
Da der Umfang der zentrischen Streckung gleich dem Umfang der ursprünglichen Figur multipliziert mit dem Betrag des gegebenen Verhältnisses ist, gilt
.
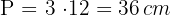6
Gegeben ist ein Trapez mit den Eckpunkten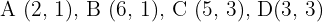 
. Berechne die Fläche der zentrischen Streckung mit dem Zentrum im Ursprung und dem Verhältnis .
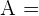
Dieses Feld ist erforderlich.
Die Fläche der zentrischen Streckung ist gleich der Fläche der ursprünglichen Figur multipliziert mit dem Quadrat des gegebenen Verhältnisses. Die Fläche des ursprünglichen Trapezes ist
.
Die Fläche der Streckung ist
.
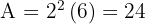7
Gegeben ist ein Stern mit den Eckpunkten .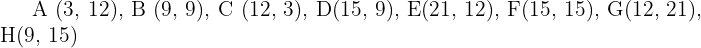
Berechne die Fläche der zentrischen Streckung mit dem Zentrum im Ursprung und dem Verhältnis 
.
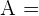
Dieses Feld ist erforderlich.
Die Fläche der zentrischen Streckung ist gleich der Fläche der ursprünglichen Figur multipliziert mit dem Quadrat des gegebenen Verhältnisses. Die Fläche des ursprünglichen Sterns besteht aus einem Quadrat mit der Seitenlänge 
und vier gleichschenkligen Dreiecken, die an jeder Seite des Quadrats ansetzen und eine Höhe von haben
.
Die Fläche der zentrischen Streckung ist
.
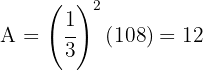8
Die zentrische Streckung des Dreiecks mit den Eckpunkten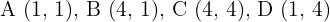 
ist ein Dreieck mit den Eckpunkten 
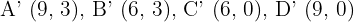. Ermittle das Verhältnis und das Zentrum der Streckung.
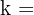
Dieses Feld ist erforderlich.
Da die Figuren zentrisch gestreckt sind, ist das Verhältnis zwischen dem Umfang der gestreckten Figur und dem Umfang der ursprünglichen Figur im Betrag gleich dem Streckungsverhältnis
Der Umfang des Quadrats mit den Eckpunkten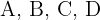 
ist 
.
Der Umfang des Quadrats mit den Eckpunkten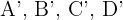 
ist .
Das Streckungsverhältnis (im Betrag) ist 
.
Um das Vorzeichen des Streckungsverhältnisses zu ermitteln, nehmen wir zwei parallele Seiten zwischen beiden Figuren. Wenn die Orientierung gleich bleibt, ist das Vorzeichen positiv. Andernfalls ist das Vorzeichen negativ. Für die Vektoren mit den Extremwerten 
und 
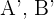gilt:
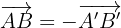
Somit ist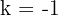 
.
, 
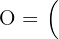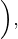
Dieses Feld ist erforderlich.
Das Zentrum der Streckung fällt mit dem Mittelpunkt der Eckpunkte und seinen Abbildungen zusammen. Für 
und 
gilt
.
9
Die zentrische Streckung eines Dreiecks mit den Eckpunkten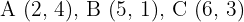 
ist ein Dreieck mit den Eckpunkten 
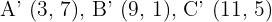. Ermittle das Verhältnis und das Zentrum der Streckung.
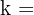
Dieses Feld ist erforderlich.
Da die Figuren zentrisch gestreckt sind, ist das Verhältnis der parallelen Seiten im Betrag gleich dem Streckungsverhältnis.
Die Seite 
ist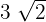 
.
Die Seite 
ist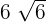 
.
Das Verhältnis der Streckung (im Betrag) ist
.
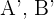Um das Vorzeichen des Streckungsverhältnisses zu ermitteln, nehmen wir zwei parallele Seiten zwischen beiden Figuren. Wenn die Orientierung gleich bleibt, ist das Vorzeichen positiv. Andernfalls ist das Vorzeichen negativ. Für die Vektoren mit den Extremwerten und gilt
Somit ist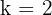 
.
,
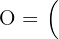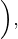
Dieses Feld ist erforderlich.
Das Zentrum der Streckung bildet zusammen mit die Extremwerte des Segments, dessen Mittelpunkt ist. Somit
.
10
Gegeben ist ein Kreis mit dem Mittelpunkt 
und dem Radius 
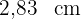. Berechne seine zentrische Streckung, wenn du weißt, dass das Zentrum der Streckung im Ursprung liegt und das Verhältnis 
ist.
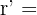
Dieses Feld ist erforderlich.
Das Verhältnis ist . Daher genügt es, die Koordinaten des Kreismittelpunkts mit zu multiplizieren, um die Koordinaten des gestreckten Kreises zu erhalten. Der Radius des neuen Kreises bleibt gleich, das heißt, er misst .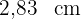
,
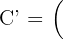Dieses Feld ist erforderlich.
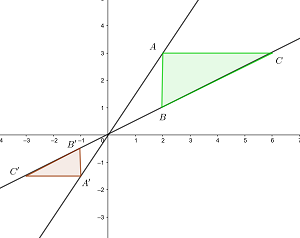
Beachte, dass ein beliebiger Punkt auf dem Kreis in sein Gegenstück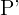 
transformiert wird, wie in der Abbildung zu sehen ist.
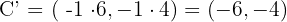
Wenn zwei Kreise konzentrisch sind, haben sie dann dasselbe Streckungszentrum?
Und wenn sie sich nicht überschneiden?
Dieses Feld ist erforderlich.
Wenn die Kreise konzentrisch sind, ist ihr Streckungszentrum identisch, während es bei sich nicht überschneidenden Kreisen nicht identisch ist. Das Streckungszentrum ist der Punkt, an dem sich die äußeren Tangenten schneiden.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
