Die Ableitung mit der Kettenregel wird angewandt, wenn wir eine Zusammensetzung von Funktionen ableiten wollen.
Wenn wir eine zusammengesetzte Funktion der Form
haben,
ist ihre Ableitung, in Bezug auf 
, gegeben durch
oder in Differentialschreibweise
Es ist zu beachten, dass 
die Ableitung von 
ist, aber in Bezug auf 
.
Die Beweisführung würde per Definition folgendermaßen aussehen
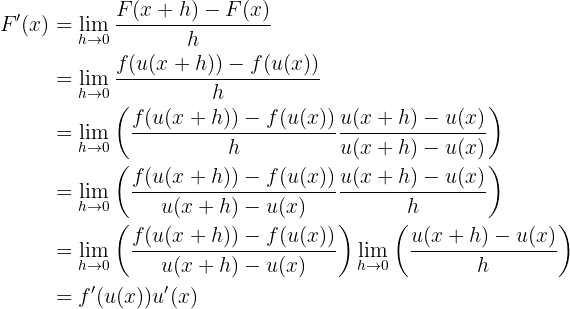
Nun sehen wir uns einige Übungen an, bei denen wir die Kettenregel anwenden.
Leite die folgende Funktion ab
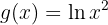
In diesem Fall können wir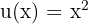 
und 
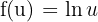nehmen. Somit:
während
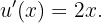
Unsere Ableitung lautet
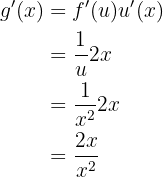
Leite die folgende Funktion ab
In diesem Fall können wir 
und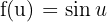 
. Así, tenemos que
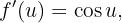
während
Unsere Ableitung lautet
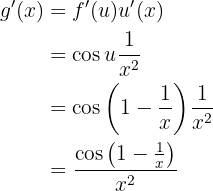
Leite die folgende Funktion ab
Es handelt sich um eine doppelte Zusammensetzung, so dass wir die Kettenregel zweimal anwenden werden. Erster Schritt:
,
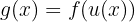wobei 
und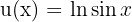 
. Somit:
Nun leiten wir 
ab. Allerdings können wir auch als Zusammensetzung ausdrücken, wobei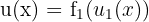 
, 
und 
. Ihre Ableitungen sind
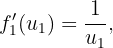
während
Unsere Ableitung lautet
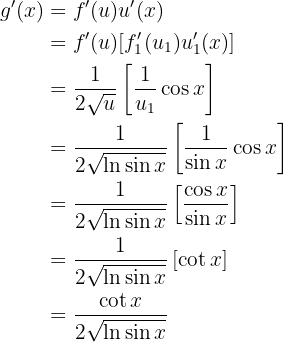
Leite die folgende Funktion ab
In diesem Fall können wir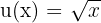 
und 
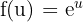nehmen. Somit:
während
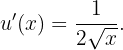
Unsere Ableitung lautet
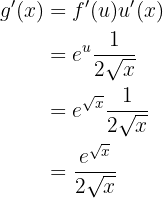
Leite die folgende Funktion ab
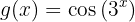
In diesem Fall können wir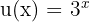 
und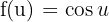 
nehmen. Somit
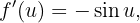
während
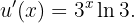
Unsere Ableitung lautet
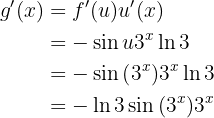
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
