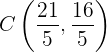Kapitel

Definition der Komponenten eines Vektors
Wir sehen uns die Punkte 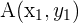 und
und 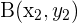 sowie den Vektor
sowie den Vektor  der vom Punkt
der vom Punkt  zum Punkt
zum Punkt  geht. Hierzu folgende Abbildung:
geht. Hierzu folgende Abbildung:
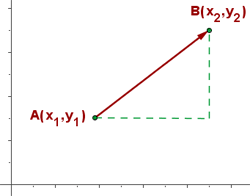
Wir definieren die Komponenten des Vektors  als Koordinaten des Endpunkts
als Koordinaten des Endpunkts  minus die Koordinaten des Startpunkts
minus die Koordinaten des Startpunkts  . Das heißt:
. Das heißt:

Vektoren werden manchmal in folgender Form geschrieben
 ,
,
wobei  die erste Komponente und
die erste Komponente und  die zweite Komponente ist. Somit
die zweite Komponente ist. Somit

A  und
und  sind auch als kanonische Vektoren bekannt. Dies ist nur eine andere Art, einen Vektor zu schreiben.
sind auch als kanonische Vektoren bekannt. Dies ist nur eine andere Art, einen Vektor zu schreiben.
Im Allgemeinen können die Bestandteile eines Vektors auch als Koordinaten bezeichnet werden. Dies ist jedoch in diesem Zusammenhang nicht angebracht. Der Grund dafür ist, dass die Koordinaten Zahlen sind, die es uns ermöglichen, ein Objekt in der Ebene oder im Raum zu finden, während die Komponenten des Vektors uns nicht dabei helfen, es in der Ebene zu lokalisieren.
Anwendung in Bezug auf die Kollinearität von Punkten
Wir haben die drei Punkte 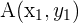 ,
, 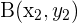 und
und 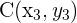 . Anhand von Vektoren können wir dann feststellen, ob diese Punkte kollinear sind (d. h. alle drei Punkte liegen auf derselben Geraden).
. Anhand von Vektoren können wir dann feststellen, ob diese Punkte kollinear sind (d. h. alle drei Punkte liegen auf derselben Geraden).
Hierbei ist zu beachten, dass zwei Vektoren parallel sind, wenn der eine das skalare Vielfache des anderen ist. Das heißt, 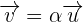 . Deshalb sind
. Deshalb sind  ,
,  und
und  kollinear, wenn
kollinear, wenn
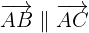
Das heißt:

Wenn wir seine Komponenten einsetzen, erhalten wir

Das heißt:

Wenn wir dann beide Gleichungen nach  auflösen, erhalten wir
auflösen, erhalten wir
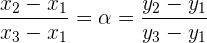
Daher sind drei Punkte kollinear, wenn gilt:

Aufgaben
Berechne die Komponenten des Vektors  , dessen Anfangs- und Endpunkte die Punkte
, dessen Anfangs- und Endpunkte die Punkte
 sind
sind
Wir wenden einfach die Formel an, die wir zu Beginn erhalten haben:
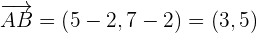
Ein Vektor  hat die Komponenten
hat die Komponenten  . Ermittle die Koordinaten von
. Ermittle die Koordinaten von  , wenn du weißt, dass
, wenn du weißt, dass 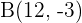 .
.
In diesem Fall betrachten wir beliebige Komponenten für  . Das heißt
. Das heißt 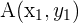 . Wir wenden also die Formel an und erhalten
. Wir wenden also die Formel an und erhalten

Daher müssen die Komponenten gleich sein, d. h:

Wenn wir nach  und
und  auflösen, erhalten wir
auflösen, erhalten wir

Somit ist  .
.
Wir haben die Punkte  ,
, 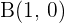 und
und 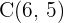 . Sind diese Punkte kollinear?
. Sind diese Punkte kollinear?
Um herauszufinden, ob die Punkte kollinear sind, überprüfen wir einfach, ob die zuvor geprüfte Relation erfüllt ist. Zunächst prüfen wir das Verhältnis der  -Komponenten:
-Komponenten:
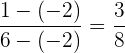
und überprüfen nun das Verhältnis der  -Komponenten :
-Komponenten :
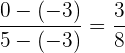
Da die beiden Verhältnisse gleich sind, kann man also davon ausgehen, dass die Punkte kollinear sind.
Wir haben die Punkte  ,
, 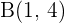 und
und 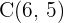 . Sind diese Punkte kollinear?
. Sind diese Punkte kollinear?
Um herauszufinden, ob die Punkte kollinear sind, überprüfen wir ähnlich wie bei der vorherigen Aufgabe, ob die Relation, die wir zuvor geprüft haben, erfüllt ist. Zunächst sehen wir uns das Verhältnis der  -Komponenten an:
-Komponenten an:
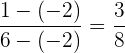
Und nun das Verhältnis der  -Komponenten:
-Komponenten:
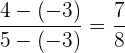
In diesem Fall sind die Anteile nicht gleich, daher sind die Punkte nicht kollinear.
Ermittle den Wert von  so, dass die Punkte
so, dass die Punkte  ,
,  und
und 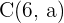 kollinear sind.
kollinear sind.
Wenn die Punkte kollinear sind, muss gelten

Auf der linken Seite der Gleichung erhalten wir
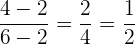
Wenn wir die Gleichung mit 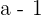 multiplizieren, erhalten wir
multiplizieren, erhalten wir

Das heißt,  .
.
Gegeben sind die Punkte  und
und 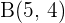 . Finde einen Punkt
. Finde einen Punkt  , der kollinear mit den Punkten
, der kollinear mit den Punkten  und
und  ist. Außerdem muss der Vektor
ist. Außerdem muss der Vektor 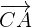
 -mal so lang sein wie
-mal so lang sein wie 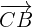 . Das heißt:
. Das heißt:

Wir haben:

, weshalb die Punkte kollinear sind. Wir bezeichnen den Punkt  als
als 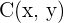 und somit
und somit

Es muss also gelten, dass
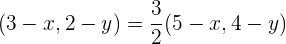
Daraus ergeben sich die folgenden Gleichungen:
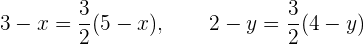
Wir lösen und erhalten: 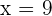 und
und 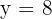 . Somit ist der Punkt
. Somit ist der Punkt 
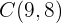
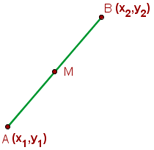
Mittelpunkt von zwei Punkten und Schwerpunkte
Wir denken daran, dass wenn wir die Punkte  und
und  haben, der Mittelpunkt dieser Punkte wie folgt berechnet wird:
haben, der Mittelpunkt dieser Punkte wie folgt berechnet wird:

Die folgende Abbildung zeigt den Mittelpunkt von  und
und  :
:
Außerdem heißt der Punkt  symmetrisch zu
symmetrisch zu  in Bezug auf
in Bezug auf  , wenn
, wenn  der Mittelpunkt der Strecke
der Mittelpunkt der Strecke  ist.
ist.
Wenn wir einen Punkt  finden wollen, der den Geradenabschnitt so teilt, dass er
finden wollen, der den Geradenabschnitt so teilt, dass er
 erfüllt,
erfüllt,
wenden wir an:
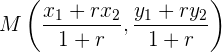
Ähnlich verhält es sich bei einem Dreieck mit den Eckpunkten 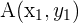 ,
, 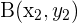 und
und 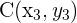 : Die Koordinaten des Schwerpunkts sind
: Die Koordinaten des Schwerpunkts sind
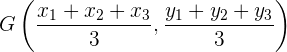
Aufgaben
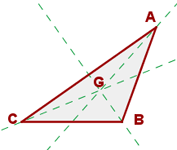
Die folgende Abbildung zeigt den Schwerpunkt eines Dreiecks:
Berechne die Koordinaten des Mittelpunkts der Strecke  , wobei
, wobei 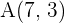 und
und 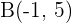 .
.
Berechne die Koordinaten des Mittelpunkts der Strecke  , wobei
, wobei 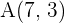 und
und 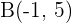 .
.
Berechne:
a den Symmetriepunkt von 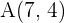 in Bezug auf den Punkt
in Bezug auf den Punkt 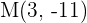 ,
,
b den Symmetriepunkt von 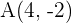 in Bezug auf den Punkt
in Bezug auf den Punkt 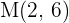 .
.
a Wir bezeichnen den Symmetriepunkt von  als
als  . Somit ist
. Somit ist  der Mittelpunkt der Strecke
der Mittelpunkt der Strecke  . Wenn also
. Wenn also  die Koordinaten
die Koordinaten 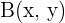 hat, dann wird
hat, dann wird  wie folgt berechnet
wie folgt berechnet
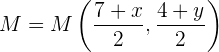
Außerdem haben wir 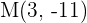 . Somit:
. Somit:
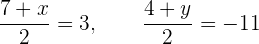
Wenn wir beide Gleichungen mit 2 multiplizieren, erhalten wir

Wenn wir also lösen, erhalten wir  und
und 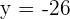 . Somit ist der Symmetriepunkt
. Somit ist der Symmetriepunkt 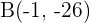 .
.
b Analog dazu bezeichnen wir den Symmetriepunkt als 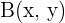 . Also berechnen wir
. Also berechnen wir  wie folgt
wie folgt
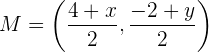
Außerdem haben wir 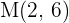 , weshalb
, weshalb
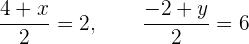
Wenn wir beide Gleichungen mit 2 multiplizieren, erhalten wir

Wir lösen und erhalten  und
und 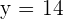 . Der Symmetriepunkt lautet somit
. Der Symmetriepunkt lautet somit 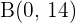 .
.
Bestimme die Koordinaten des Schwerpunkts für:
a ein Dreieck mit den Eckpunkten 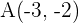 ,
, 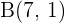 und
und  ,
,
b ein Dreieck mit den Eckpunkten  ,
,  und
und  .
.
In dieser Aufgabe brauchen wir nur die Formel für den Schwerpunkt eines Dreiecks zu verwenden. Also:
a Für den ersten Punkt gilt
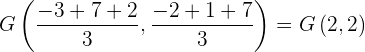
b Für den zweiten Punkt gilt

Berechne die Punkte  und
und  , die die Strecke
, die die Strecke  mit den Anfangs- und Endpunkten
mit den Anfangs- und Endpunkten  und
und 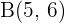 in drei gleiche Teile teilen.
in drei gleiche Teile teilen.
Wir stellen fest, dass wir die Punkte  und
und  bestimmen müssen
bestimmen müssen
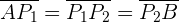
1 Um den ersten Punkt zu bestimmen, beachten wir:
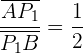 ,
,
da die Strecke des Nenners doppelt so groß ist. Wir verwenden also die Formel:
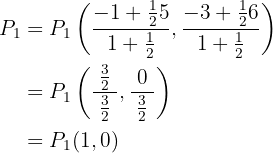
2 Für den zweiten Punkt gilt:
 ,
,
da in diesem Fall die Strecke des Zählers doppelt so groß ist. Wir verwenden also die Formel:
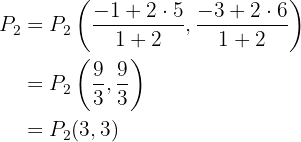
Somit lauten die Punkte  und
und  .
.
Ermittle die Koordinaten des Punkts  .
. 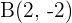 ist hierbei der Mittelpunkt von
ist hierbei der Mittelpunkt von  und gegeben ist der Punkt
und gegeben ist der Punkt 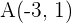 .
.
Wir schreiben die Koordinaten des Punkts  als
als 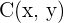 . Somit wird
. Somit wird  wie folgt berechnet
wie folgt berechnet
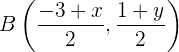
Außerdem haben wir 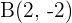 . Und somit die Gleichungen
. Und somit die Gleichungen

Wenn wir die Gleichungen mit 2 multiplizieren, erhalten wir

Wenn wir also lösen, erhalten wir  und
und 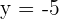 . Somit lautet der Punkt
. Somit lautet der Punkt
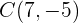
Sieh dir die Strecke  mit den Anfangs- und Endpunkten
mit den Anfangs- und Endpunkten 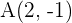 und
und  an. Bestimme die Koordinaten des Punkts
an. Bestimme die Koordinaten des Punkts  , der die Strecke
, der die Strecke  in zwei Teile teilt.
in zwei Teile teilt.  ist die Hälfte von
ist die Hälfte von  .
.
Da  die Hälfte von
die Hälfte von  ist, erhalten wir
ist, erhalten wir
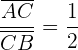
Wir wenden also die Formel an:
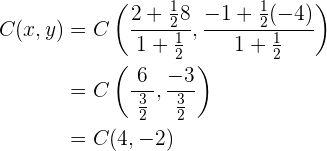
Somit lautet der Punkt 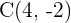 .
.
Wenn die Strecke  mit den Anfangs- und Endpunkten
mit den Anfangs- und Endpunkten 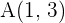 und
und 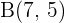 in vier gleiche Teile geteilt wird, wie lauten dann die Koordinaten der jeweiligen Punkte?
in vier gleiche Teile geteilt wird, wie lauten dann die Koordinaten der jeweiligen Punkte?
Wir suchen die 3 Punkte  ,
,  und
und  sowie
sowie
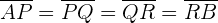
Sieh dir hierzu folgende Abbildung an:
1 Für die Berechnung von  gilt:
gilt:
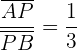 ,
,
da die Strecke von  nach
nach  ein Drittel der Strecke von
ein Drittel der Strecke von  nach
nach  beträgt. Wir wenden also die Formel an, um
beträgt. Wir wenden also die Formel an, um  zu berechnen:
zu berechnen:
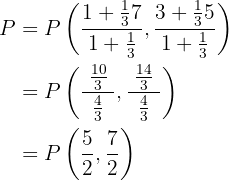
2 Wir stellen fest, dass  der Mittelpunkt zwischen
der Mittelpunkt zwischen  und
und  . Wir berechnen also wie folgt:
. Wir berechnen also wie folgt:
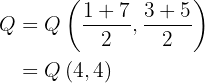
3 Für  erhalten wir schließlich
erhalten wir schließlich
 ,
,
da die Strecke von  nach
nach  dreimal so lang ist wie die Strecke von
dreimal so lang ist wie die Strecke von  nach
nach  . Wir verwenden also die Formel, um
. Wir verwenden also die Formel, um  zu berechnen:
zu berechnen:
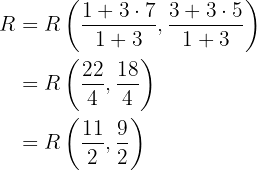
Deshalb lauten die Punkte
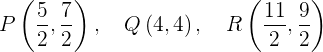
Betrachten wir ein Dreieck, dessen zwei Eckpunkte  und
und 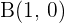 sind. Wenn der Schwerpunkt des Dreiecks der Punkt
sind. Wenn der Schwerpunkt des Dreiecks der Punkt  ist, wie lauten dann die Koordinaten des dritten Eckpunkts
ist, wie lauten dann die Koordinaten des dritten Eckpunkts  ?
?
Wir bezeichnen die Koordinaten von  als
als 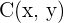 . Somit wied der Schwerpunkt wie folgt berechnet
. Somit wied der Schwerpunkt wie folgt berechnet

Wir haben aber auch  , weshalb
, weshalb
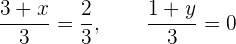
Wir multiplizieren mit 3 und erhalten

Daraus folgt, dass  und
und  . Somit ist der Eckpunkt
. Somit ist der Eckpunkt  der Punkt
der Punkt

Gegeben sind die Punkte  und
und 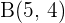 . Finde einen Punkt
. Finde einen Punkt  , der kollinear mit den Punkten
, der kollinear mit den Punkten  und
und  ist, und für den gilt:
ist, und für den gilt:

Die Formel, die wir für Mittelpunkte oder Punkte, die eine Strecke in einem bestimmten Verhältnis teilen, haben, wird immer für kollineare Punkte verwendet. Daher wenden wir diese Formel an.
Außerdem haben wir bereits das Verhältnis  , sodass wir die Formel anwenden können:
, sodass wir die Formel anwenden können:
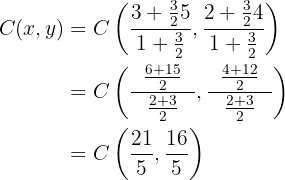
Somit ist der Punkt