Kapitel

Wie wird der Mittelpunkt einer Strecke bestimmt?
Als Beispiel nehmen wir die Strecke  mit den Endpunkten
mit den Endpunkten 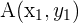 und
und 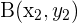 der folgenden Abbildung:
der folgenden Abbildung:
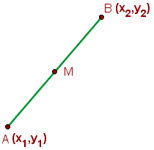
Der Mittelpunkt ist der Punkt  , der sich auf der Strecke
, der sich auf der Strecke  befindet und bewirkt, dass die Strecke
befindet und bewirkt, dass die Strecke  genauso lang ist wie die Strecke
genauso lang ist wie die Strecke 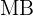 , das heißt
, das heißt
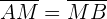
Der Mittelpunkt wird anhand folgender Formel berechnet:

Man sagt, der Punkt  ist der Spiegelpunkt von
ist der Spiegelpunkt von  an
an  , wenn
, wenn  der Mittelpunkt der Strecke
der Mittelpunkt der Strecke  ist.
ist.
Punkte, die eine Strecke proportional teilen
Wenn wir einen Punkt  ermitteln wollen, der eine Strecke so teilt, dass die Bedingung
ermitteln wollen, der eine Strecke so teilt, dass die Bedingung

erfüllt ist, verwenden wir
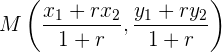
Rechenaufgaben: Koordinaten des Mittelpunkts
Bestimme die Koordinaten des Mittelpunkts der Strecke  mit den Endpunkten:
mit den Endpunkten:
a 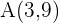 und
und  ,
,
b 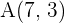 und
und 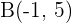 .
.
Um den Mittelpunkt zu bestimmen, verwende einfach die Formel:
a Für den ersten Fall erhältst du
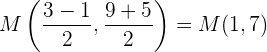
Der Mittelpunkt ist daher 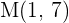 .
.
b Für den zweiten Fall ist der Mittelpunkt
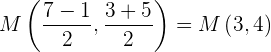
Berechne:
a den Spiegelpunkt von 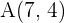 an
an 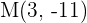
b den Spiegelpunkt von 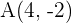 an
an 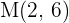
a Wir benennen den Spiegelpunkt von  mit
mit  .
.  ist der Mittelpunkt der Streckees
ist der Mittelpunkt der Streckees  . Wenn
. Wenn  die Koordinaten
die Koordinaten 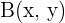 hat, berechnet sich
hat, berechnet sich  mit
mit
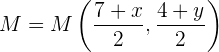
Außerdem ist 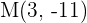 . Daher ist
. Daher ist
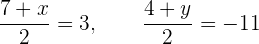
Wenn wir beide Gleichungen mit 2 multiplizieren, erhalten wir

Wir lösen auf und erhalten  und
und 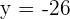 . Der Spiegelpunkt ist also
. Der Spiegelpunkt ist also 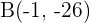 .
.
b Benenne den Spiegelpunkt wie in der vorherigen Aufgabe mit 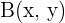 .
.  wird wie folgt berechnet:
wird wie folgt berechnet:
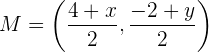
Außerdem ist 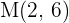 . Daher ist
. Daher ist
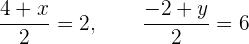
Wenn wir beide Gleichungen mit 2 multiplizieren, erhalten wir

Wir lösen auf und erhalten  und
und 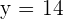 . Der Spiegelpunkt ist also
. Der Spiegelpunkt ist also 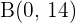 .
.
Berechne die Punkte  und
und  die die Strecke
die die Strecke  mit den Endpunkten
mit den Endpunkten  und
und 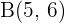 in drei gleich lange Segmente teilen.
in drei gleich lange Segmente teilen.
Wir müssen die beiden Punkte  und
und  so definieren, dass
so definieren, dass
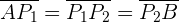
a Um den ersten Punkt zu finden, muss
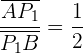 sein,
sein,
da das Segment, das im Nenner steht, die doppelte Länge haben muss. Wende nun die Formel an:
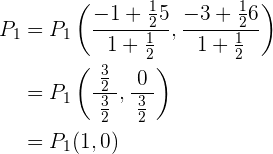
b Um den zweiten Punkt zu finden, gehen wir ähnlich vor:
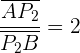 ,
,
da in diesem Fall das Segment des Zählers doppelt so lang ist. Wende nun die Formel an:
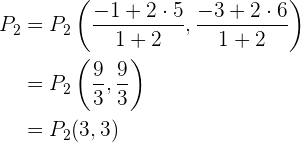
Die Punkte sind also  und
und 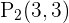 .
.
Ermittle die Koordinaten des Punktes  .
. 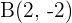 ist dabei der Mittelpunkt von
ist dabei der Mittelpunkt von  und
und 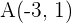 .
.
Notiere die Koordinaten des Punktes  als
als 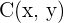 .
.  erhält man dann wie folgt:
erhält man dann wie folgt:
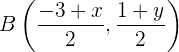
Außerdem ist 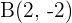 . Daher erhalten wir zwei Gleichungen
. Daher erhalten wir zwei Gleichungen

Wenn wir beide Gleichungen mit 2 multiplizieren, erhalten wir

Wir lösen auf und erhalten  y
y 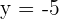 . Der gesuchte Punkt ist also
. Der gesuchte Punkt ist also
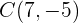
Gegeben sei die Strecke  mit den Endpunkten
mit den Endpunkten 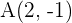 und
und  Bestimme die Koordinaten des Punktes
Bestimme die Koordinaten des Punktes  , der die Strecke
, der die Strecke  so in zwei Segmente teilt, dass
so in zwei Segmente teilt, dass  halb so lang wie
halb so lang wie  ist.
ist.
Da  halb so lang wie
halb so lang wie  sein muss, erhalten wir
sein muss, erhalten wir
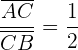
Verwende die Formel:
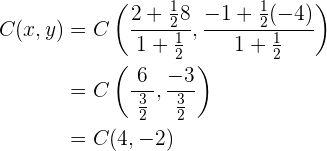
Der gesuchte Punkt ist also 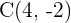 .
.
Die Strecke  mit den Endpunkten
mit den Endpunkten 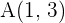 und
und 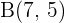 wird in vier gleich lange Teile geteilt. Welche Koordinaten haben die Punkte, die sie teilen?
wird in vier gleich lange Teile geteilt. Welche Koordinaten haben die Punkte, die sie teilen?
Wir suchen die Punkte  ,
,  und
und  , für die
, für die
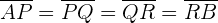
wie in der folgenden Abbildung gezeigt wird:
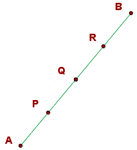
a Um  zu berechnen, gehen wir wie folgt vor:
zu berechnen, gehen wir wie folgt vor:
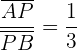 ,
,
da die Strecke von  zu
zu  ein Drittel der Länge der Strecke von
ein Drittel der Länge der Strecke von  zu
zu  misst. Um
misst. Um  zu berechnen, verwenden wir also folgende Formel:
zu berechnen, verwenden wir also folgende Formel:
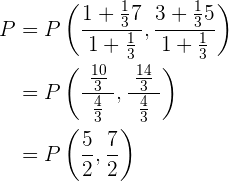
b Wir sehen, dass  der Mittelpunkt zwischen
der Mittelpunkt zwischen  und
und  ist, daher wird er wie folgt berechnet:/p>
ist, daher wird er wie folgt berechnet:/p>
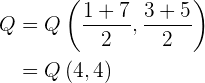
c Zuletzt erhalten wir für 
 ,
,
da die Strecke von  nach
nach  drei mal so lang sein muss wie die Strecke von
drei mal so lang sein muss wie die Strecke von  nach
nach  . Anhand der Formel erhalten wir für
. Anhand der Formel erhalten wir für  :
:
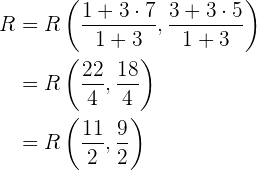
Die gesuchten Punkte sind also
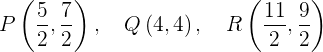
Gegeben seien die Punkte  und
und 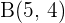 . Bestimme den Punkt
. Bestimme den Punkt  , der kolinear zu
, der kolinear zu  und
und  ist und folgendes erfüllt:
ist und folgendes erfüllt:

Für die Berechnung von kolinearen Punkten wird immer die Formel zur Berechnung der Mittelpunkte oder der Punkte, die eine Strecke teilen, verwendet:
Die Beziehung  der Punkte zueinander steht auch bereits fest, daher können wir die Formel verwenden:
der Punkte zueinander steht auch bereits fest, daher können wir die Formel verwenden:
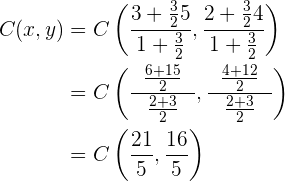
Der gesuchte Punkt  ist also
ist also
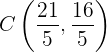
Mit KI zusammenfassen:













