Kapitel

Definition von karthesischen Koordinaten und Polarkoordinaten
In einem orthonormalen Bezugssystem entspricht jedem Punkt  in der Ebene ein Vektor
in der Ebene ein Vektor 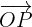 , so dass:
, so dass:
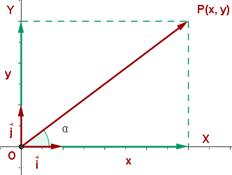
Der Vektor 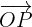 wird normalerweise wie folgt dargestellt:
wird normalerweise wie folgt dargestellt:
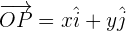
Die Koeffizienten  und
und  der Linearkombination werden als die Koordinaten des Punktes
der Linearkombination werden als die Koordinaten des Punktes  bezeichnet. Die Koordinate
bezeichnet. Die Koordinate  heißt Abszisse und die Koordinate
heißt Abszisse und die Koordinate  Ordinate.
Ordinate.
Da die Linearkombination eindeutig ist, entspricht jeder Punkt einem Zahlenpaar und jedes Zahlenpaar einem Punkt.
Wenn der Betrag des Vektors  und der Winkel
und der Winkel  , der mit der Achse
, der mit der Achse  gebildet wird, bekannt sind, sagt man, dass der Vektor mit Polarkoordinaten angegeben ist.
gebildet wird, bekannt sind, sagt man, dass der Vektor mit Polarkoordinaten angegeben ist.
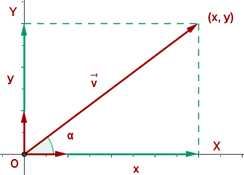
Umwandeln von Koordinaten
Um polare in kartesische Koordinaten umzuwandeln, nutzen wir die folgenden Formeln:


Beispiel: 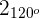 in karthesische Koordianten umwandeln
in karthesische Koordianten umwandeln
1 Wir haben  und
und 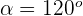
2 Wir berechnen die Koordinate 

3 Wir berechnen die Koordinate 

In karthesischen Koordinaten ausgedrückt lautet der Ausdruck
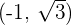
Um kartesische in polare Koordinaten umzuwandeln, nutzen wir die folgenden Formeln:
Betrag
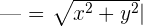
Argument oder Winkel
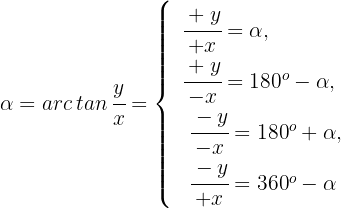
Beispiel: in Polarkoordianten umwandeln
in Polarkoordianten umwandeln
1 Wir haben  und
und 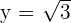
2 Wir berechnen den Betrag

3 Wir berechnen das Argument
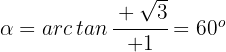
In Polarkoordinaten ausgedrückt lautet der Ausdruck
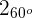
Aufgaben zu karthesischen Koordinaten und Polarkoordinaten
Wandle die folgenden in Polarkoordinaten ausgedrückten Vektoren in kartesische Koordinaten um

1 Wir haben 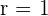 und
und 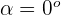
2 Wir berechnen die Koordinate 
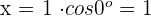
3 Wir berechnen die Koordinate 
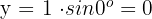
Der Ausdruck in kartesischen Koordinaten lautet also

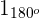
1 Wir haben 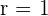 und
und 
2 Wir berechnen die Koordinate 
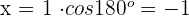
3 Wir berechnen die Koordinate 
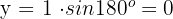
Der Ausdruck in kartesischen Koordinaten lautet also

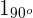
1 Wir haben 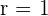 und
und 
2 Wir berechnen die Koordinate 

3 Wir berechnen die Koordinate 
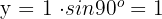
Der Ausdruck in kartesischen Koordinaten lautet also

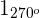
1 Wir haben 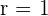 und
und 
2 Wir berechnen die Koordinate 
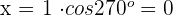
3 Wir berechnen die Koordinate 

Der Ausdruck in kartesischen Koordinaten lautet also

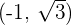
1 Tenemos que  y
y 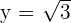
2 Wir berechnen den Betrag
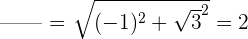
3 Wir berechnen das Argument
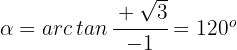
Der Ausdruck in Polarkoordinaten lautet also
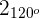
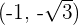
1 Wir haben  und
und 
2 Wir berechnen den Betrag

3 Wir berechnen das Argument
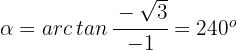
Der Ausdruck in Polarkoordinaten lautet also
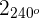
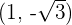
1 Wir haben  und
und 
2 Wir berechnen den Betrag
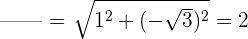
3 Wir berechnen das Argument
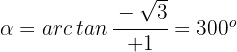
Der Ausdruck in Polarkoordinaten lautet also


1 Wir haben  und
und 
2 Wir berechnen den Betrag
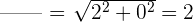
3 Wir berechnen das Argument
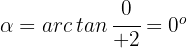
Der Ausdruck in Polarkoordinaten lautet also
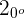
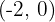
1 Wir haben  und
und 
2 Wir berechnen den Betrag
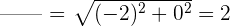
3 Wir berechnen das Argument

Der Ausdruck in Polarkoordinaten lautet also


1 Wir haben  und
und 
2 Wir berechnen den Betrag
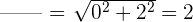
3 Wir berechnen das Argument
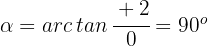
Der Ausdruck in Polarkoordinaten lautet also
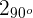
Mit KI zusammenfassen:












