Kapitel

Definition
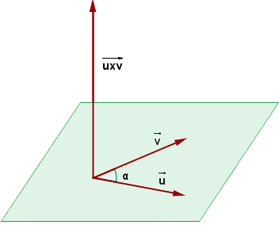
Das Vektorprodukt  aus zwei Vektoren ist ein weiterer Vektor, der in die entgegengesetzte Richtung zu den zwei Vektoren verläuft. Seine Orientierung kann mit einem Korkenzieher verglichen werden, der von
aus zwei Vektoren ist ein weiterer Vektor, der in die entgegengesetzte Richtung zu den zwei Vektoren verläuft. Seine Orientierung kann mit einem Korkenzieher verglichen werden, der von 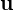 nach
nach 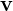 gedreht wird. Sein Betrag entspricht:
gedreht wird. Sein Betrag entspricht:
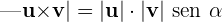
Das Vektorprodukt kann als Determinante geschrieben werden:
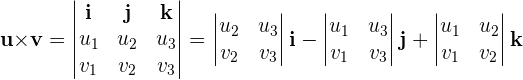
Beispiele
Berechne das Vektorprodukt der Vektoren  und
und 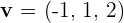 .
.
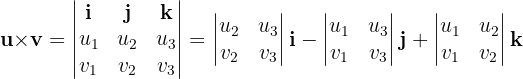
1 In die Formel einsetzen
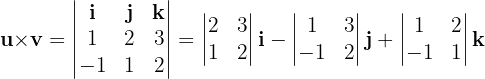
2 Die Determinanten von  berechnen
berechnen
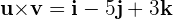
Gegeben sind die Vektoren y
y  . Berechne das Vektorprodukt dieser Vektoren. Beweise, dass der ermittelte Vektor orthogonal zu
. Berechne das Vektorprodukt dieser Vektoren. Beweise, dass der ermittelte Vektor orthogonal zu 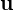 und
und 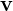 ist.
ist.
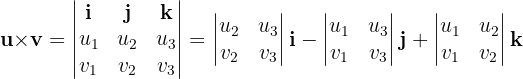
1 In die Formel einsetzen
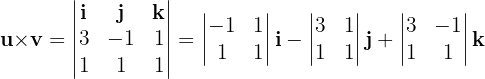
2 Die Determinanten von  berechnen
berechnen

3 Orthogonalität mithilfe des Skalarprodukts überprüfen
Wir berechnen das Skalarprodukt des resultierenden Vektors mit 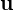 und
und 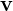
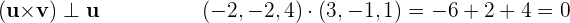
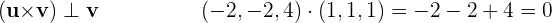
Da das Ergebnis null ist, ist das Vektorprodukt  orthogonal zu den Vektoren
orthogonal zu den Vektoren 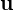 und
und 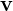 .
.
Fläche des Parallelogramms
Geometrisch gesehen entspricht der Betrag des Vektorprodukts zweier Vektoren der Fläche des Parallelogramms mit diesen Vektoren als Seiten
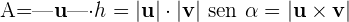
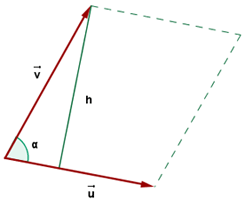
Beispiel
Gegeben sind die Vektoren 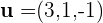 und
und  . Bestimme die Fläche des Parallelogramms, dessen Seiten die Vektoren
. Bestimme die Fläche des Parallelogramms, dessen Seiten die Vektoren 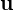 und
und 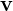 sind.
sind.
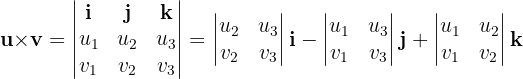
1 In die Formel einsetzen
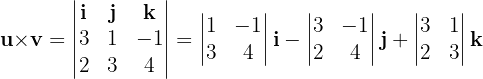
2 Die Determinante von  berechnen
berechnen

3 Die Fläche des Parallelogramms bestimmen
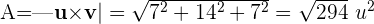
Fläche eines Dreiecks
Die Diagonale eines Parallelogramms teilt dieses in zwei gleiche Dreiecke. Somit ist die Fläche des Dreiecks die Hälfte der Fläche des Parallelogramms.
Beispiel
Bestimme die Fläche des Dreiecks mit den Eckpunkten



1 Die Vektoren ermitteln, die die Seiten des Dreicks bilden
Folgende Vektoren bilden die Seiten:

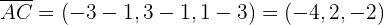
2 In die Formel zur Berechnung des Vektorprodukts einsetzen
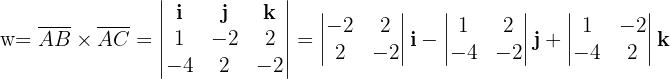
3 Die Determinante von  berechnen
berechnen

Als Koordinaten ausgedrückt:
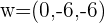
4 Wir berechnen die Fläche
Wir berechnen den Betrag des resultierenden Vektors des Vektorprodukts
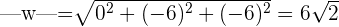
Wir dividieren durch zwei
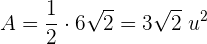
Eigenschaften des Vektorprodukts
1 Antikommutativität
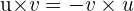
2 Es gilt die Regel

3 Für das Vektorprodukt gilt das Distributivgesetz
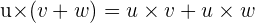
4 Das Vektorprodukt zweier paralleler Vektoren entspricht dem Nullvektor.

5 Das Vektorprodukt  ist senkrecht zu
ist senkrecht zu  und zu
und zu  .
.


Mit KI zusammenfassen:













