Kapitel

Was versteht man unter linear abhängigen Vektoren?
Mehrere freie Vektoren der Ebene (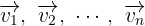 ) sind linear abhängig, wenn es eine Linearkombination aus ihnen gibt, die gleich dem Nullvektor (
) sind linear abhängig, wenn es eine Linearkombination aus ihnen gibt, die gleich dem Nullvektor (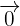 ) entspricht, ohne dass alle Koeffizienten (
) entspricht, ohne dass alle Koeffizienten ( ) der Linearkombination null sind.
) der Linearkombination null sind. 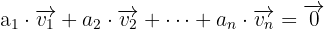
Hinweis: Der Nullvektor bezieht sich auf einen Vektor, der den Betrag 0 hat und dessen Komponenten alle 0 sind. Er wird mit 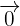 bezeichnet.
bezeichnet.
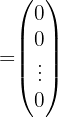
Eigenschaften linear abhängiger Vektoren
1 Wenn mehrere Vektoren linear abhängig sind, kann mindestens einer von ihnen als lineare Kombination der anderen ausgedrückt werden.
Um dies zu veranschaulichen, betrachten wir die linear abhängigen Vektoren 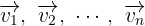 . Da sie linear abhängig sind, können wir schreiben:
. Da sie linear abhängig sind, können wir schreiben: 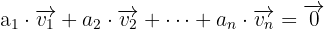
Nun subtrahieren wir den Vektor 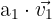 auf beiden Seiten und erhalten:
auf beiden Seiten und erhalten: 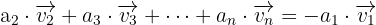
Nun dividieren wir durch 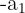 (hierfür nehmen wir an, dass
(hierfür nehmen wir an, dass  )
)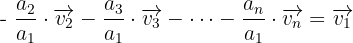
Schließlich schreiben wir um und nehmen zu besseren Veranschaulichung 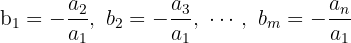 . Wir haben also:
. Wir haben also: 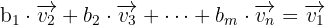
Letztendlich kommen wir also zu dem Schluss, dass wir einen Vektor tatsächlich als Linearkombination der anderen ausdrücken können.
Das Gegenteil trifft ebenfalls zu: Wenn ein Vektor eine Linearkombination aus anderen Vektoren ist, dann sind alle Vektoren linear abhängig.
2 Zwei Vektoren sind genau dann linear abhängig, wenn sie parallel sind.
Um die Richtigkeit dieser Aussage zu überprüfen, betrachten wir zwei Vektoren  und
und  . Dabei nehmen wir an, dass die parallel sind, weshalb es eine Zahl
. Dabei nehmen wir an, dass die parallel sind, weshalb es eine Zahl 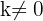 gibt, sodass:
gibt, sodass: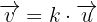
Somit können wir 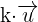 auf beiden Seiten der Gleichung subtrahieren und erhalten:
auf beiden Seiten der Gleichung subtrahieren und erhalten: 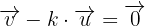
Wir haben also eine Linearkombination der Vektoren  und
und  , wobei die Koeffizienten ungleich 0 sind. Daher sind die Vektoren per Definition linear abhängig.
, wobei die Koeffizienten ungleich 0 sind. Daher sind die Vektoren per Definition linear abhängig.
3 Zwei freie Vektoren 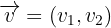 und
und 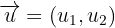 sind linear abhängig, wenn ihre Elemente zueinander proportional sind.
sind linear abhängig, wenn ihre Elemente zueinander proportional sind.
Dies folgt direkt aus der vorherigen Eigenschaft, da die Elemente der Vektoren zueinander proportional sind, wenn es eine Zahl  gibt, sodass gilt:
gibt, sodass gilt: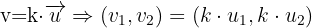
Beispiel für eine Übung mit linear abhängigen Vektoren
Berechne die Werte von  , sodass die Vektoren
, sodass die Vektoren 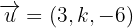 ,
, 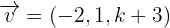 und
und 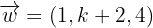 linear abhängig sind. Schreibe
linear abhängig sind. Schreibe  als Linearkombination von
als Linearkombination von  und
und 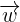 , wobei
, wobei  der berechnete Wert ist.
der berechnete Wert ist.
Vektoren sind linear abhängig, wenn die Determinante der von ihnen gebildeten Matrix null ist, d. h. wenn der Rang der Matrix kleiner als  ist.
ist.
Wir setzen die Determinante also gleich  und lösen nach
und lösen nach  auf
auf
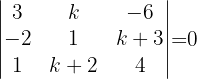

Wenn wir die allgemeine Formel für quadratische Gleichungen verwenden, erhalten wir folgende Werte: 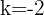 und
und 
Um den zweiten Teil zu lösen, verwenden wir den Wert von 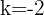 .
.
Wir müssen also zwei Zahlen  und
und  finden, sodass:
finden, sodass:
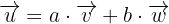
Somit haben wir das folgende System:
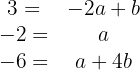
Aus der zweiten Gleichung erhalten wir 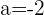 . Wenn wir diesen Wert also in die dritte Gleichung einsetzen, erhalten wir:
. Wenn wir diesen Wert also in die dritte Gleichung einsetzen, erhalten wir:

Also lautet die Linearkombination:
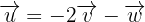
Mit KI zusammenfassen:












