Linearkombination
Eine Linearkombination zweier Vektoren ist der Vektor, den man erhält, wenn man diese Vektoren mit einem Skalar multipliziert und dann addiert.
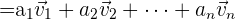
Jeder Vektor kann als Linearkombination von anderen Vektoren mit unterschiedlichen Richtungen dargestellt werden.
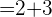
Diese Linearkombination ist eindeutig bestimmt.
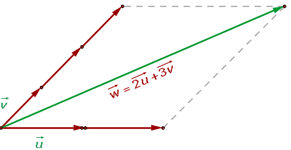
Linear abhängige Vektoren
Mehrere freie Vektoren in der Ebene gelten als linear abhängig, wenn es eine Linearkombination von ihnen gibt, die gleich dem Nullvektor ist, ohne dass alle Koeffizienten der Linearkombination gleich null sind.
Eigenschaften
1 Wenn mehrere Vektoren linear abhängig sind, kann mindestens einer von ihnen als Linearkombination der anderen ausgedrückt werden.
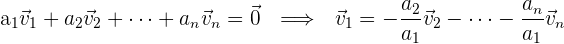
Auch der Umkehrschluss gilt: Wenn ein Vektor eine Linearkombination anderer Vektoren ist, dann sind alle Vektoren linear abhängig.
2 Zwei Vektoren der Ebene sind nur dann linear abhängig, wenn sie parallel sind.
3 Zwei freie Vektoren der Ebene 
sind linear abhängig, wenn ihre Komponenten proportional sind.
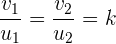
4 
Vektoren des 
sind linear abhängig, wenn die Determinante null ist.
Beispiel:
Bestimme die Werte für 
so, dass die Vektoren 
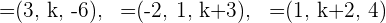linear abhängig sind. Schreibe 
als Linearkombination von 
und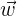 
, wobei der berechnete Wert ist.
Die Vektoren sind linear abhängig, wenn die Determinante der Matrix, die sie bilden, null ist. Der Rang der Matrix ist also kleiner als 3.
1Wir berechnen die Determinante
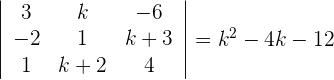
2Wir setzen die Determinante gleich null
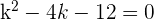
3Wir lösen die Gleichung und erhalten
4Für 
sind die Vektoren somit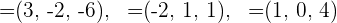 
. Wir schreiben in Bezug auf und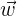
5Wir berechnen die Werte für die Skalare 
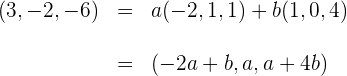
6Wenn wir die Koordinaten der linken Seite mit denen der rechten Seite gleichsetzen und die Gleichungen lösen, erhalten wir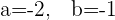 
7Somit ist die gesuchte Linearkombination
8Wir wiederholen die Schritte 4, 5, 6 und 7 für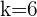 
Linear unabhängige Vektoren
Mehrere freie Vektoren sind linear unabhängig, wenn keiner von ihnen als Linearkombination der übrigen geschrieben werden kann, sodass, wenn die Linearkombination gleich null ist, auch jeder ihrer Koeffizienten gleich null ist.
Die linear unabhängigen Vektoren haben eine unterschiedliche Richtung und ihre Komponenten sind nicht proportional.
Vektoren des sind linear unabhängig, wenn die Determinante ungleich null ist.
Beispiel:
Untersuche, ob die Vektoren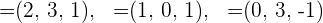 
linear abhängig oder unabhängig sind.
1 Wir berechnen die Determinante der Vektoren
2Da die Determinante null ist, schließen wir daraus, dass die Vektoren linear abhängig sind
Basis
Drei Vektoren 
mit unterschiedlicher Richtung bilden eine Basis, da jeder Vektor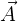 
des Vektorraums, als Linearkombination von ihnen dargestellt werden kann
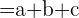
Die Koordinaten des Vektors in Bezug auf die Basis sind:
Orthogonalbasis
Eine Basis ist orthogonal, wenn die Vektoren der Basis zueinander senkrecht sind.
Orthonormalbasis
Eine Basis ist orthonormal, wenn die Vektoren der Basis zueinander senkrecht sind und ihr Betrag 1 ist.
Die Basis, die die Vektoren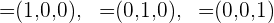 
bilden, wird Standardbasis genannt.
Beispiel:
Für welche Werte von 
bilden die Vektoren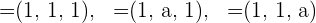 
eine Basis?
1 Wir berechnen die Determinante der Vektoren
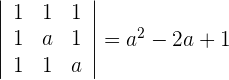
2Die Determinante ist null für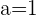 
. Die Vektoren sind also linear abhängig und bilden keine Basis, wenn .
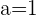3Die Determinante ist ungleich null für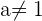 
. Die Vektoren sind also linear unabhängig und bilden eine Basis, wenn .
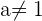Du findest diesen Artikel toll? Vergib eine Note!
Loading...
