Der Begriff der Basis ist einer der wichtigsten in der linearen Algebra. Im Grunde ist eine Basis eine Teilmenge von Elementen unseres Vektorraums, mit der wir alle Vektoren in Form dieser Elemente ausdrücken können. Zunächst beachten wir, dass drei Vektoren  ,
,  und
und 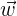 im Raum linear unabhängig sind, wenn einer von ihnen nicht als Linearkombination der anderen beiden Vektoren geschrieben werden kann.
im Raum linear unabhängig sind, wenn einer von ihnen nicht als Linearkombination der anderen beiden Vektoren geschrieben werden kann.
Das bedeutet, dass die drei Vektoren unterschiedliche Richtungen haben. Außerdem bilden die drei Vektoren  ,
,  und
und 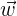 den gesamten Raum, wenn ein beliebiger Vektor
den gesamten Raum, wenn ein beliebiger Vektor  als Linearkombination aus
als Linearkombination aus  ,
,  und
und 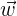 geschrieben werden kann. Das heißt,
geschrieben werden kann. Das heißt, 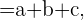 , wobei
, wobei  ,
,  und
und  reelle Zahlen sind.
reelle Zahlen sind.
Schließlich definieren wir eine Basis des Raums als eine Menge von drei Elementen  ,
,  und
und 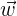 so dass sie linear unabhängig sind und den gesamten Raum bilden.
so dass sie linear unabhängig sind und den gesamten Raum bilden.
Das bekannteste Beispiel für eine Basis aus drei Vektoren ist die Standardbasis
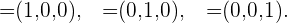
Die Koordinaten eines beliebigen Vektors  lauten also wie folgt
lauten also wie folgt
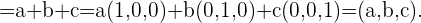

Orthogonalbasis
Eine Basis der Vektoren  ,
,  und
und 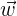 ist orthogonal, wenn die Vektoren der Basis zueinander senkrecht sind. Das heißt:
ist orthogonal, wenn die Vektoren der Basis zueinander senkrecht sind. Das heißt:
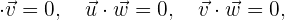 ,
,
wobei  das Skalarprodukt darstellt.
das Skalarprodukt darstellt.
Die Standardbasis ist eine Orthogonalbasis, da ihre Elemente senkrecht zueinander stehen.
Orthonormalbasis
Eine Basis ist orthonormal, wenn die Vektoren der Basis senkrecht zueinander stehen und außerdem den Betrag 1 haben. Das heißt,

Auch hier können wir sagen, dass die Standardbasis orthonormal ist, da
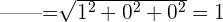
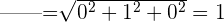
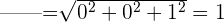
Beispiele für orthogonale und orthonormale Basen
1 Gegeben sind die Vektoren 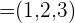 ,
, 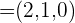 und
und  . Zeige, dass diese Vektoren eine Basis bilden und berechne die Koordinaten des Vektors
. Zeige, dass diese Vektoren eine Basis bilden und berechne die Koordinaten des Vektors  in Bezug auf diese Basis.
in Bezug auf diese Basis.
Wir stellen fest, dass diese Vektoren linear sind, also stellen wir die folgende Gleichung auf
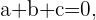

Daraus ergibt sich das folgende Gleichungssystem
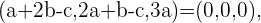
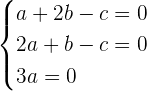
Um herauszufinden, wie viele Lösungen dieses System hat, müssen wir seine Determinante berechnen. Wenn diese ungleich 0 ist, haben wir nur die einfache Lösung 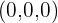
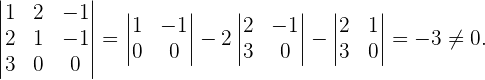
Das homogene System lässt nur die einfache Lösung zu:

Daher sind die drei Vektoren linear unabhängig und bilden eine Basis.
Nun suchen wir die Koordinaten des Vektors  in Bezug auf unsere Basis. Dazu stellen wir die folgende Gleichung auf, wobei
in Bezug auf unsere Basis. Dazu stellen wir die folgende Gleichung auf, wobei  ,
,  und
und  reelle Zahlen sind
reelle Zahlen sind
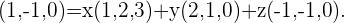
Daraus ergibt sich das folgende Gleichungssystem, aus dem wir die Lösungen für  ,
,  und erhalten, die die gesuchten Koordinaten darstellen
und erhalten, die die gesuchten Koordinaten darstellen
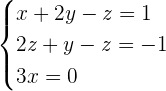
Wir erhalten  und somit ist
und somit ist 
Daraus folgt, dass 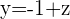
und 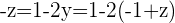
sowie 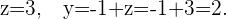
Daher sind die Koordinaten von  in unserer Basis
in unserer Basis 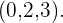
2 Gegeben sind die Vektoren: 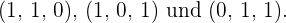
A Zeige, dass sie eine Basis bilden.
Die drei Vektoren bilden eine Basis, wenn sie linear unabhängig sind. Um dies zu zeigen, stellen wir die folgende Gleichung und das folgende System auf

Daraus ergibt sich das folgende Gleichungssystem
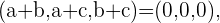
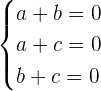
Um herauszufinden, wie viele Lösungen dieses System hat, müssen wir seine Determinante berechnen. Wenn diese ungleich 0 ist, haben wir nur die einfache Lösung 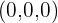 ,
,
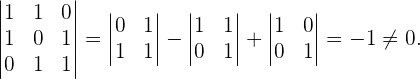
Das homogene System lässt nur die einfache Lösung zu:

Daher sind die drei Vektoren linear unabhängig und bilden eine Basis.
B Ermittle die Koordinaten der Vektoren der Standardbasis in Bezug auf diese.
Um dies zu lösen, müssen wir die folgenden drei Gleichungen aufstellen
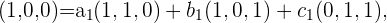
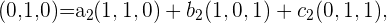

Und die Werte für alle 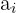 ,
, 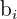 und
und 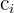 bestimmen. Diese bestimmen die Koordinaten für die Vektoren der Standardbasis. Wir beginnen mit der ersten Gleichung, aus der wir das folgende Gleichungssystem erhalten
bestimmen. Diese bestimmen die Koordinaten für die Vektoren der Standardbasis. Wir beginnen mit der ersten Gleichung, aus der wir das folgende Gleichungssystem erhalten
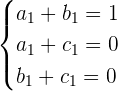
Wir stellen fest, dass 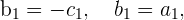
weshalb 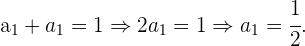
Und somit 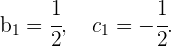
Die Koordinaten des Vektors 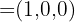 lauten also
lauten also  Aus der zweiten Gleichung ergibt sich das folgende Gleichungssystem
Aus der zweiten Gleichung ergibt sich das folgende Gleichungssystem
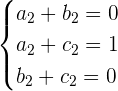
Wir stellen fest, dass 
weshalb 
Und somit 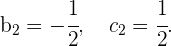
Die Koordinaten des Vektors 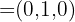 lauten also
lauten also 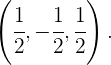 Aus der letzten Gleichung ergibt sich das folgende Gleichungssystem
Aus der letzten Gleichung ergibt sich das folgende Gleichungssystem
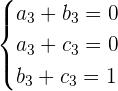
Wir stellen fest, dass 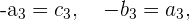
weshalb 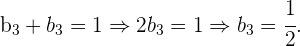
Und somit 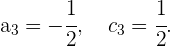
Die Koordinaten des Vektors 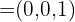 lauten also
lauten also 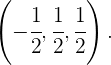
C Berechne den Wert von  so, dass die Vektoren
so, dass die Vektoren 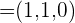 ,
, 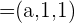 und
und 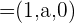 eine Basis bilden.
eine Basis bilden.
Es gilt zu beachten, dass diese Vektoren linear unabhängig sind. Wir überprüfen dies, indem wir die Determinanten der durch sie gebildeten Matrix berechnen. Wenn die Determinante ungleich 0 ist, sind sie linear unabhängig
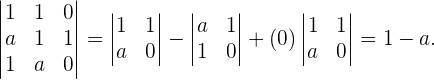
Diese Determinante ist ungleich 0, wenn 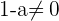 . Das heißt
. Das heißt  Daraus lässt sich schließen, dass die Vektoren eine Basis bilden, wenn
Daraus lässt sich schließen, dass die Vektoren eine Basis bilden, wenn 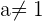 .
.
Mit KI zusammenfassen:












