Gegeben sind die Vektoren:
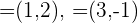
Ermittle die Linearkombination:

Als Erstes setzen wir die Werte von  ,
, 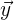 in die Linearkombination ein und erhalten:
in die Linearkombination ein und erhalten: 
Nun multiplizieren wir mit dem Skalar:

Wir müssen also die Summe der Vektoren bilden, um das Problem zu lösen:
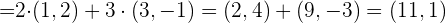
Kann der Vektor  als Linearkombination der Vektoren
als Linearkombination der Vektoren  ,
, 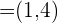 ausgedrückt werden?
ausgedrückt werden?
Um herauszufinden, ob es möglich ist, den Vektor 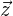 als Linearkombination der Vektoren
als Linearkombination der Vektoren  ,
, 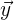 auszudrücken, müssen wir Skalare
auszudrücken, müssen wir Skalare  ,
,  finden, so dass:
finden, so dass: 
Wenn wir die Werte von  einsetzen, erhalten wir:
einsetzen, erhalten wir:
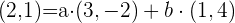
Dies ist gleichbedeutend mit dem Lösen des Gleichungssystems;
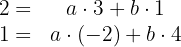
Um dies zu lösen, nehmen wir die erste Gleichung und lösen nach  auf. Wir erhalten:
auf. Wir erhalten:
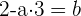
Nun setzen wir den Wert von  in die 2. Gleichung ein und erhalten:
in die 2. Gleichung ein und erhalten:
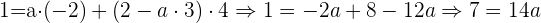
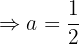
Daraus folgt: 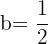 .
.
Wir konnten die Skalare  ,
,  ermitteln, so dass:
ermitteln, so dass:

Der Vektor 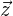 kann also als Linerarkombination der Vektoren
kann also als Linerarkombination der Vektoren  ,
, 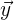 ausgedrückt werden.
ausgedrückt werden.
Welche Paare der folgenden Vektoren bilden eine Basis für die Ebene  ?
?
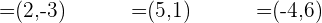
Da wir nach einer Basis für die  -Ebene suchen, wissen wir, dass zwei Vektoren eine Basis bilden, wenn sie nicht linear abhängig sind. Und wir wissen wiederum, dass zwei Vektoren linear abhängig sind, wenn einer ein skalares Vielfaches des anderen ist. Das heißt, es genügt zu prüfen, ob in einem Paar von Vektoren keiner von ihnen ein Vielfaches des anderen ist, damit sie eine Basis bilden.
-Ebene suchen, wissen wir, dass zwei Vektoren eine Basis bilden, wenn sie nicht linear abhängig sind. Und wir wissen wiederum, dass zwei Vektoren linear abhängig sind, wenn einer ein skalares Vielfaches des anderen ist. Das heißt, es genügt zu prüfen, ob in einem Paar von Vektoren keiner von ihnen ein Vielfaches des anderen ist, damit sie eine Basis bilden.
Bei zwei Vektoren 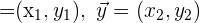 sagen wir, dass einer ein Vielfaches des anderen ist, wenn
sagen wir, dass einer ein Vielfaches des anderen ist, wenn 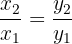
Wir nehmen also die Vektoren 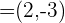 und
und 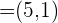 . Wir stellen fest:
. Wir stellen fest:
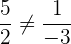
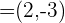 und
und 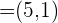 bilden daher eine Basis für die Ebene.
bilden daher eine Basis für die Ebene.
Nun nehmen wir die Vektoren 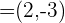 und
und  . Wir stellen fest:
. Wir stellen fest:
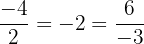
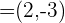 und
und  bilden daher keine Basis für die Ebene.
bilden daher keine Basis für die Ebene.
Zuletzt nehmen wir die Vektoren 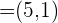 und
und  und stellen fest:
und stellen fest:
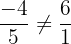
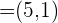 y
y  bilden daher eine Basis für die Ebene.
bilden daher eine Basis für die Ebene.
Finde einen Einheitsvektor  , der die gleiche Richtung hat wie der Vektor
, der die gleiche Richtung hat wie der Vektor 
Die Formel für die Bestimmung eines Einheitsvektors  mit der gleichen Richtung wie ein Vektor
mit der gleichen Richtung wie ein Vektor  ist gegeben durch:
ist gegeben durch: 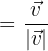
Dabei stellt  die Norm des Vektors
die Norm des Vektors  dar.
dar.
Wir setzen die gegebenen Werte ein und erhalten:
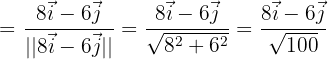
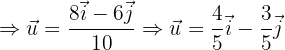
Angenommen, die Vektoren  haben in Bezug auf die Orthonormalbasis
haben in Bezug auf die Orthonormalbasis 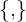 der Ebene die Ausdrücke:
der Ebene die Ausdrücke:

Berechne den Wert von  , wenn du weißt, dass
, wenn du weißt, dass 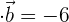
Wir setzen die jeweiligen Werte von 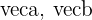 in den Ausdruck
in den Ausdruck 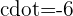 ein. So erhalten wir schließlich:
ein. So erhalten wir schließlich: 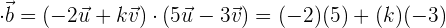
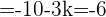
Wenn wir also das  des letzten Ausdrucks ermitteln, erhalten wir:
des letzten Ausdrucks ermitteln, erhalten wir:
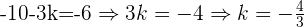
Gegeben sind die Vektoren  und
und 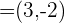 . Berechne
. Berechne  , so dass die Vektoren
, so dass die Vektoren  und
und  folgende Eigenschaften erfüllen:
folgende Eigenschaften erfüllen:
- Sie sind zueinander senkrecht.
- Sie sind parallel.
- Sie bilden einen Winkel von
 .
.
a Wenn wir möchten, dass die Vektoren senkrecht zueinander stehen, müssen wir einen Wert für  wählen, der:
wählen, der: 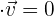
Setzt man die Werte der beiden Vektoren in die letztgenannte Gleichung ein und führt die entsprechenden Rechenschritte durch, erhält man: 
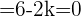
Wenn wir also  berechnen, erhalten wir:
berechnen, erhalten wir:
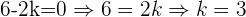
b Die Forderung, dass zwei Vektoren parallel sein sollen, ist gleichbedeutend mit der Forderung, dass einer der Vektoren ein skalares Vielfaches des anderen sein soll. Also müssen wir einen Wert für  wählen, für den gilt, dass:
wählen, für den gilt, dass: 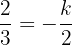
Diesen können wir leicht erhalten, indem wir  aus diesem letzten Ausdruck ermitteln. Wir erhalten:
aus diesem letzten Ausdruck ermitteln. Wir erhalten: 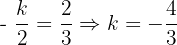
c Der Winkel, der von zwei Vektoren 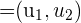 und
und  gebildet wird, ist durch folgenden Ausdruck gegeben:
gebildet wird, ist durch folgenden Ausdruck gegeben: 
Dabei steht 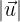 für die Norm des Vektors
für die Norm des Vektors  (ähnlich für
(ähnlich für  ) und
) und  ist der Winkel zwischen den Vektoren. Wenn wir also einen Winkel zwischen den Vektoren suchen, der
ist der Winkel zwischen den Vektoren. Wenn wir also einen Winkel zwischen den Vektoren suchen, der  ist, bedeutet dies, dass:
ist, bedeutet dies, dass:
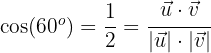
Wir setzen den Wert von  und
und  in diesen letzten Ausdruck ein und erhalten:
in diesen letzten Ausdruck ein und erhalten:
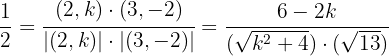
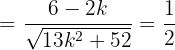
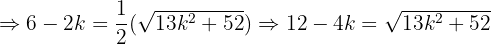
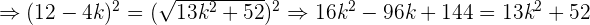

Nun müssen wir nur noch die allgemeine Formel für quadratische Gleichungen anwendne und erhalten so die Lösungen des letzten Ausdrucks:

Bestimme  , wenn der Winkel, den
, wenn der Winkel, den 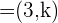 mit
mit 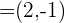 bildet, wie folgt ist:
bildet, wie folgt ist:
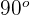 .
.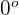 .
.- Sie bilden einen Winkel von
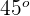 .
.
a Wenn der Winkel zwischen den Vektoren 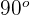 beträgt, sind die Vektoren zueinander senkrecht. Daher muss der Wert von
beträgt, sind die Vektoren zueinander senkrecht. Daher muss der Wert von  wie folgt sein:
wie folgt sein: 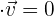
Wenn wir die Werte der beiden Vektoren in diese letzte Gleichung einsetzen und die entsprechenden Schritte durchführen, erhalten wir: 

Wenn wir also nach  auflösen, erhalten wir:
auflösen, erhalten wir:
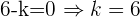
b Wenn der Winkel zwischen zwei Vektoren 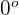 ist, bedeutet dies, dass die Vektoren parallel sind. Dies entspricht der Forderung, dass einer der Vektoren ein skalares Vielfaches des anderen Vektors sein muss, so dass wir einen Wert für
ist, bedeutet dies, dass die Vektoren parallel sind. Dies entspricht der Forderung, dass einer der Vektoren ein skalares Vielfaches des anderen Vektors sein muss, so dass wir einen Wert für  finden müssen, der:
finden müssen, der: 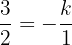
Diesen erhalten wir ganz einfach, indem wir diesen letzten Ausdruck nach  auflösen. Wir erhalten:
auflösen. Wir erhalten: 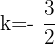
c Der Winkel, den die zwei Vektoren 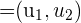 und
und  bilden, ist durch folgenden Ausdruck gegeben:
bilden, ist durch folgenden Ausdruck gegeben: 
Dabei steht 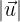 für die Norm des Vektors
für die Norm des Vektors  (ähnlich für
(ähnlich für  ), und
), und  ist der Winkel zwischen den Vektoren. Wenn der Winkel zwischen den Vektoren
ist der Winkel zwischen den Vektoren. Wenn der Winkel zwischen den Vektoren 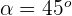 sein soll, bedeutet das:
sein soll, bedeutet das:
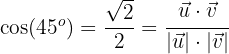
Wir setzen den Wert von  und
und  in diesen letzten Ausdruck ein und erhalten:
in diesen letzten Ausdruck ein und erhalten:
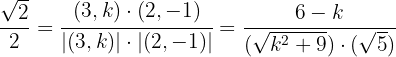
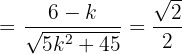
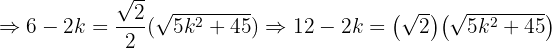


Jetzt müssen wir nur noch die allgemeine Formel für quadratische Gleichungen anwenden, um die Lösungen des letzten Ausdrucks zu finden. Diese sind:

Wir nehmen an, dass die Vektoren  und
und  in Bezug auf die Orthonormalbasis
in Bezug auf die Orthonormalbasis  der Ebene folgende Ausdrücke haben:
der Ebene folgende Ausdrücke haben:

Berechne den Wert von  , so dass die zwei Vektoren orthogonal sind.
, so dass die zwei Vektoren orthogonal sind.
Wenn zwei Vektoren  und
und  orthogonal sind, gilt:
orthogonal sind, gilt:  . Damit dies zutrifft, muss ein Wert für
. Damit dies zutrifft, muss ein Wert für  gesucht werden. Dazu setzen wir die Werte der Vektoren ein und führen die entsprechenden Rechenoperationen durch.
gesucht werden. Dazu setzen wir die Werte der Vektoren ein und führen die entsprechenden Rechenoperationen durch. 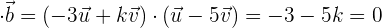
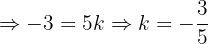
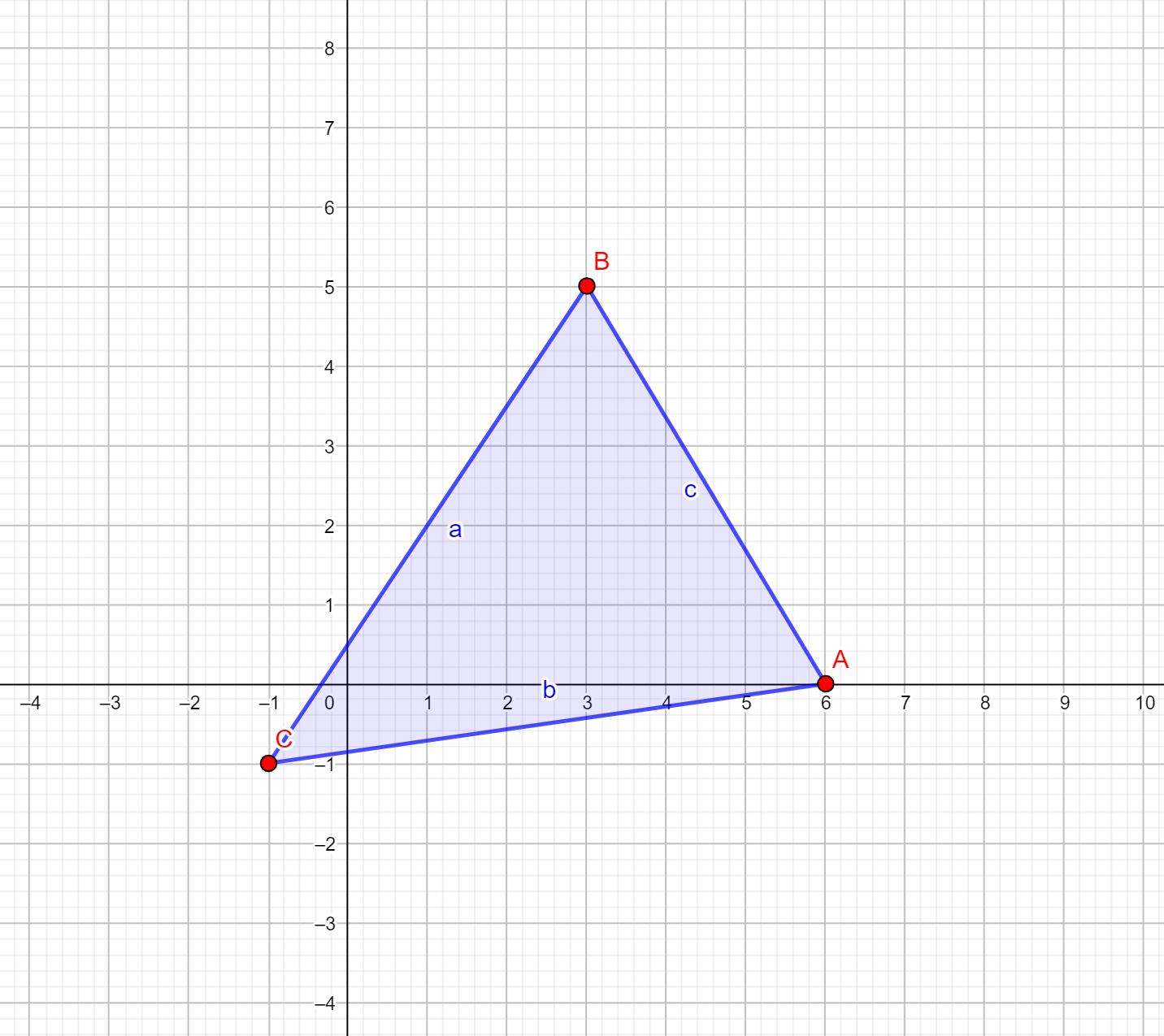
Berechne die Winkel des Dreiecks mit den Eckpunkten: 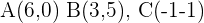
Der Winkel, den die zwei Vektoren 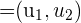 und
und  bilden, ist durch folgenden Ausdruck gegeben:
bilden, ist durch folgenden Ausdruck gegeben: 
Dabei stellt 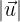 die Norm des Vektors
die Norm des Vektors  (ähnlich für
(ähnlich für  ) dar und
) dar und  ist der Winkel zwischen den Vektoren. In diesem Fall können wir die Segmente, die die Punkte des Dreiecks verbinden, wie folgt als Vektoren betrachten:
ist der Winkel zwischen den Vektoren. In diesem Fall können wir die Segmente, die die Punkte des Dreiecks verbinden, wie folgt als Vektoren betrachten: 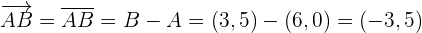

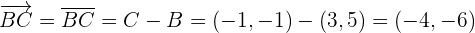
Zunächst ermitteln wir den Winkel  , der zwischen den Vektoren
, der zwischen den Vektoren  und
und  liegt, mit der anfangs genannten Formel:
liegt, mit der anfangs genannten Formel:
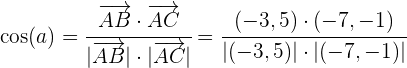
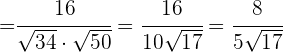
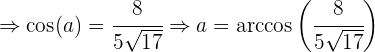
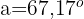
Nun bestimmen wir den Winkel  , der zwischen den Vektoren
, der zwischen den Vektoren  und
und 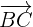 liegt, mit der anfangs genannten Formel:
liegt, mit der anfangs genannten Formel:
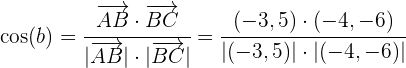

Da 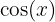 eine gerade Funktion ist, gilt
eine gerade Funktion ist, gilt  . Wir erhalten somit:
. Wir erhalten somit:
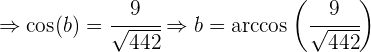
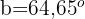
Um den Wert des letzten Winkels  zu ermitteln, können wir dasselbe Verfahren wie bei den vorherigen Winkeln anwenden, aber wir nutzen die Tatsache, dass die Summe der Innenwinkel eines Dreiecks gleich
zu ermitteln, können wir dasselbe Verfahren wie bei den vorherigen Winkeln anwenden, aber wir nutzen die Tatsache, dass die Summe der Innenwinkel eines Dreiecks gleich 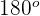 ist. Somit:
ist. Somit:
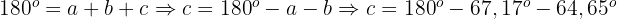
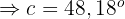
Berechne die Abbildung des Vektors  auf den Vektor
auf den Vektor 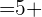 .
.
Die Abbildung des Vektors  auf den Vektor
auf den Vektor  ist durch folgende Formel gegeben:
ist durch folgende Formel gegeben: 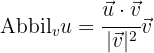 ,
,
wobei  die Norm des Vektors
die Norm des Vektors  ist. Wir setzen also die Werte der Vektoren
ist. Wir setzen also die Werte der Vektoren  und
und  in diese Formel ein und erhalten:
in diese Formel ein und erhalten: 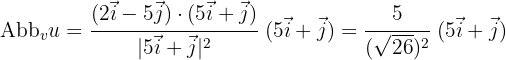
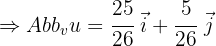
Berechne die Abbildung des Vektors  auf den Vektor
auf den Vektor  , wobei
, wobei  .
.
Als Erstes berechnen wir die Elemente der Vektoren  und
und 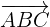 :
: 
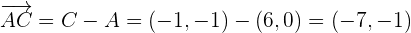
Nun ist die Abbildung des Vektors  auf den Vektor
auf den Vektor  durch die folgende Formel gegeben:
durch die folgende Formel gegeben: 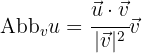
Wenn wir also die Werte der Aufgabenvektoren einsetzen, erhalten wir: 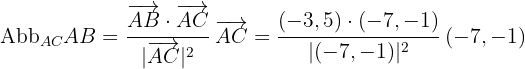
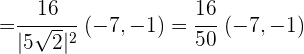
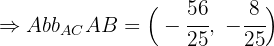
Prüfe, ob das Segment, das die Mittelpunkte der Seiten  und
und  des Dreiecks verbindet:
des Dreiecks verbindet: 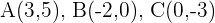 , ist parallel zur Seite
, ist parallel zur Seite  und gleich seiner Hälfte.
und gleich seiner Hälfte.
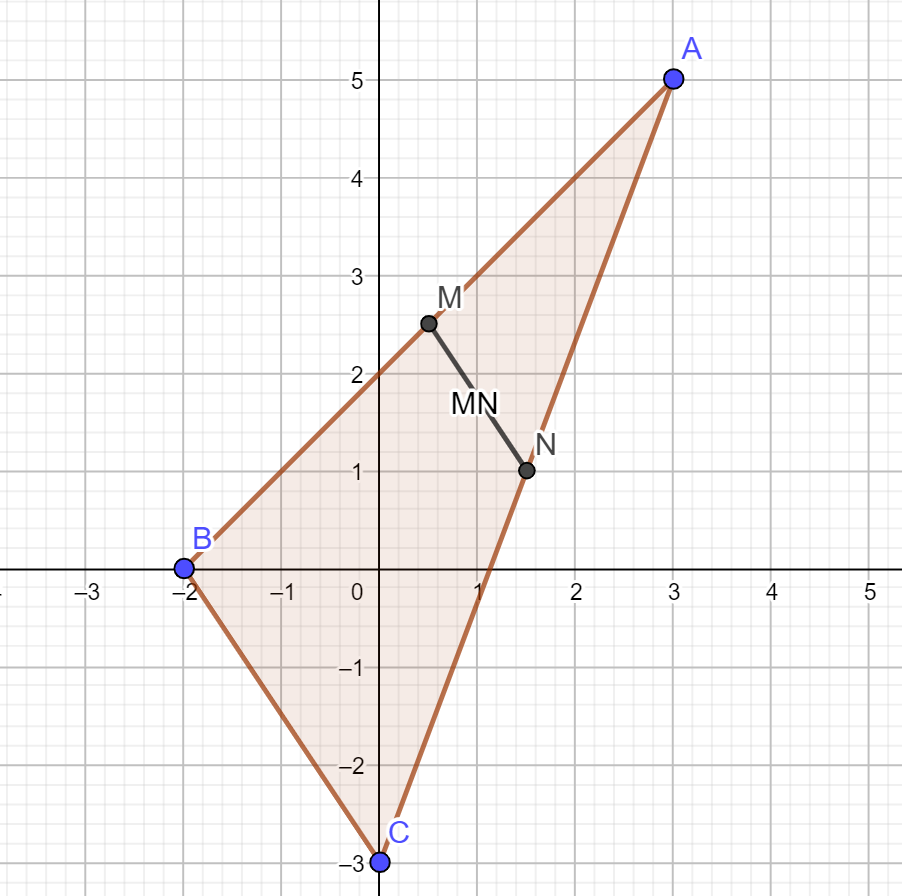
Als Erstes müssen wir den Mittelpunkt der Seiten  und
und  finden, den wir mit der folgenden Formel berechnen können:
finden, den wir mit der folgenden Formel berechnen können: 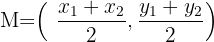
Der Mittelpunkt der Seite  ist also:
ist also: 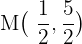
und der Mittelpunkt der Seite  ist:
ist: 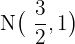
Somit ist das Segment, dass die Mittelpunkte dieser Seiten verbindet 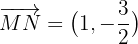 . Nun ist das Segment
. Nun ist das Segment 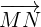 parallel zur Seite
parallel zur Seite 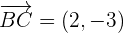 , wenn die Elemente proportional sind (das eine ist ein Vielfaches des anderen).
, wenn die Elemente proportional sind (das eine ist ein Vielfaches des anderen).
Bei den Vektoren 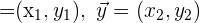 ist einer ein Vielfaches des anderen, wenn
ist einer ein Vielfaches des anderen, wenn 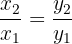
Wenn wir letzteres nutzen, können wir herausfinden, ob die Vektoren 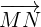 ,
, 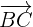 parallell sind. Also setzen wir ihre Elemente in diesen Ausdruck ein und erhalten:
parallell sind. Also setzen wir ihre Elemente in diesen Ausdruck ein und erhalten:
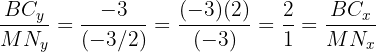
Das Segment ist also tatsächlich 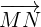 parallel zur Seite
parallel zur Seite 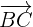 .
.
Wenn 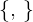 eine Orthonormalbasis bildet, berechne:
eine Orthonormalbasis bildet, berechne:
 .
.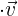 .
.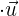 .
. .
.
Da die Vektoren  eine Orthonormalbasis bilden, bedeutet dies, dass die Norm jedes Vektors gleich
eine Orthonormalbasis bilden, bedeutet dies, dass die Norm jedes Vektors gleich  ist.
ist. 
Wir wissen nun, dass der Winkel  zwischen zwei Vektoren
zwischen zwei Vektoren  gegeben ist durch:
gegeben ist durch: 
Wir können diesen Ausdruck also wie folgt umschreiben: 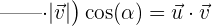
Mit dem letzten Ausdruck erhalten wir:
a 
Da wir das Punktprodukt zweier gleicher Vektoren berechnen, ist der Winkel zwischen ihnen  und ihre Norm ist
und ihre Norm ist  , da es sich um Vektoren handelt, die zur Orthonormalbasis gehören. Somit:
, da es sich um Vektoren handelt, die zur Orthonormalbasis gehören. Somit:
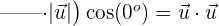

b 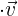
Da wir das Punktprodukt zwischen zwei Vektoren berechnen, die zur Orthonormalbasis gehören, bedeutet dies, dass der Winkel zwischen den beiden Vektoren 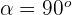 ist und die Norm
ist und die Norm  ist. Somit:
ist. Somit:
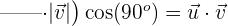
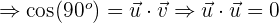
c 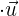
Da wir das Punktprodukt zweier Vektoren berechnen, die zur Orthonormalbasis gehören, bedeutet dies, dass der Winkel zwischen den beiden Vektoren 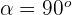 ist und seine Norm
ist und seine Norm  ist. Somit:
ist. Somit:

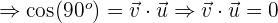
4
Da wir das Punktprodukt zwischen zwei Vektoren berechnen, die zur Orthonormalbasis gehören, bedeutet dies, dass der Winkel zwischen den beiden Vektoren  ist und seine Norm
ist und seine Norm  ist. Somit:
ist. Somit:
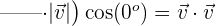
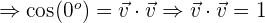
Mit KI zusammenfassen:


