Gegeben sind die Vektoren 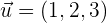 ,
, 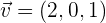 und
und 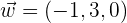 . Berechne:
. Berechne:
a
b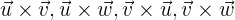
c und
und 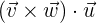
d
e und
und 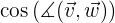
a
Bevor wir die Aufgabe lösen, sehen wir uns Folgendes zur Erinnerung an:
Wenn wir den Vektor 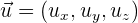 und den Vektor
und den Vektor  haben, lautet das Skalarprodukt:
haben, lautet das Skalarprodukt:
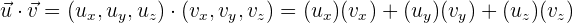
und so können wir also die Aufgabe bearbeiten.

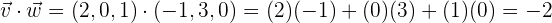
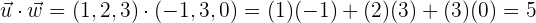
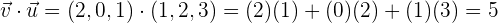
b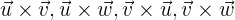
Unter Verwendung der gleichen Systematik definieren wir das Vektorprodukt wie folgt:
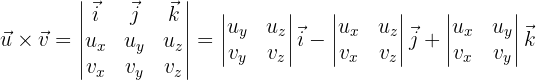
wobei
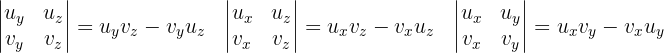
was es uns ermöglicht, die gewünschten Aufgaben zu lösen.
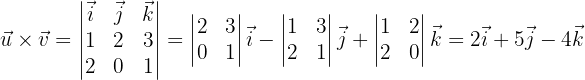
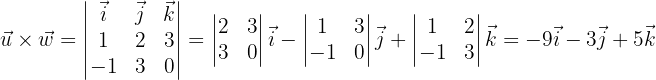
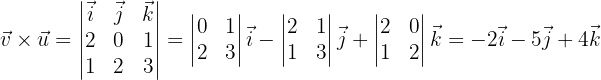
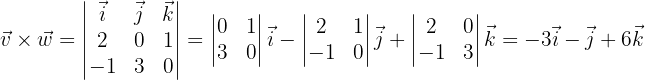
c y
y 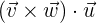
Sobald wir uns über die Definitionen von Skalar- und Vektorprodukt im Klaren sind, können wir sie kombinieren. Vergiss nicht, dass ein Skalarprodukt eine Zahl und ein Vektorprodukt einen Vektor erzeugt. Daher ist die Reihenfolge, in der die Produkte gebildet werden, wichtig, daher die Klammern. Das Endprodukt ist das Volumen des durch die Vektoren erzeugten Parallelogramms, und da die Vektoren gleich sind, ist das Volumen in beiden Fällen dasselbe.


4
Erinnern wir uns noch einmal an die Definition des Betrags eines Vektors, indem wir die ursprüngliche Systematik anwenden
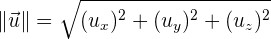
mit der Formel können wir nun berechnen
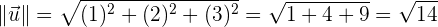

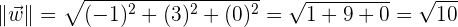
d y
y 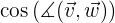
Mit all diesen Informationen ist es nun möglich, den Kosinus des zwischen den Vektoren gebildeten Winkels zu berechnen.
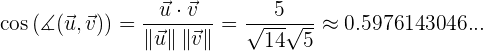

aDie Beträge von  und
und 
bDas Vektorprodukt von  und
und 
cEinen orthogonalen Einheitsvektor zu  und
und 
dDie Fläche des Parallelogramms, dessen Seiten die Vektoren  und
und  sind
sind
aDie Beträge von  und
und 

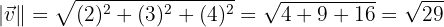
bDas Vektorprodukt von  und
und 
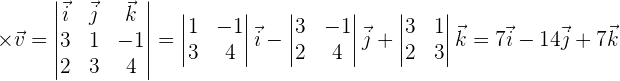
cEinen orthogonalen Einheitsvektor zu  und
und 
Bei der Berechnung des Vektorprodukts zweier Vektoren wird ein zu beiden Vektoren orthogonaler Vektor erzeugt
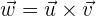
wir benötigen den orthogonalen Vektor; er muss nur noch zum Einheitsvektor werden. Wir berechnen also zunächst seinen Betrag

er wird nun zum Einheitsvektor
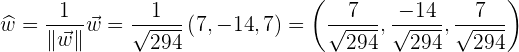
dDie Fläche des Parallelogramms, dessen Seiten die Vektoren  und
und  sind
sind
Die Fläche des Parallelogramms wird mit dem Betrag des Vektorprodukts der Vektoren, die es bilden, berechnet
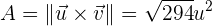
Berechne den Winkel, den die Vektoren  und
und  bilden.
bilden.
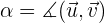
sei der Winkel zwischen den Vektoren.
Wir berechnen nun den Kosinus dieses Winkels.
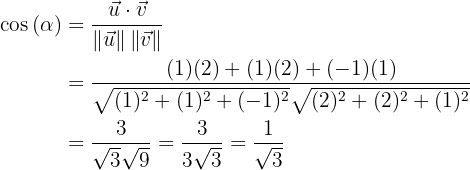
Wir wenden nun die Umkehrung des Kosinus auf den berechneten Wert an, um den Wert des Winkels zwischen den Vektoren zu ermitteln
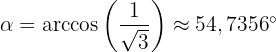
Berechne die Richtungskosinus des Vektors 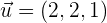 .
.
Die Richtungskosinuns werden zur Bestimmung des Winkels verwendet, der zwischen jeder Achse und dem jeweiligen Vektor entsteht, d. h. sie dienen als Hilfsmittel zur Lokalisierung eines Punktes


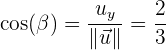

Gegeben sind die Vektoren  und
und 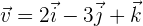 . Berechne das Produkt
. Berechne das Produkt  und überprüfe, dass dieser Vektor orthogonal zu
und überprüfe, dass dieser Vektor orthogonal zu  und
und  ist. Berechne den Vektor
ist. Berechne den Vektor 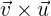 und überprüfe ihn mit
und überprüfe ihn mit  .
.
Zunächst das Vektorprodukt
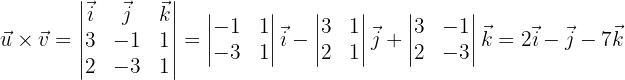
Damit zwei Vektoren senkrecht zueinander stehen, muss ihr Skalarprodukt gleich 0 sein

'Wir prüfen:

nun mit dem anderen Vektor
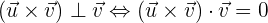
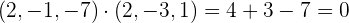
Wir stellen fest, dass die Vektoren tatsächlich senkrecht zueinander sind.
Nun berechnen wir das folgende Vektorprodukt, wobei zu beachten ist, dass die Vektoren nun unterschiedliche Ordnungen haben
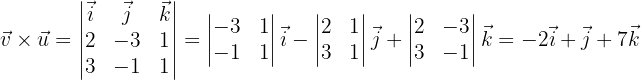
So kommt man zu einem Beispiel für eine der wichtigsten Eigenschaften des Vektorprodukts – die Antikommutativität
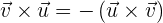
Mit KI zusammenfassen:


