Kapitel

Definition des Punktprodukts
Das Punktprodukt oder Skalarprodukt zweier Vektoren ist eine mathematische Verknüpfung, deren Ergebnis eine reelle Zahl ist. Es gibt verschiedene Möglichkeiten, diese Verknüpfung zu definieren. Eine davon ist die Multiplikation des Produkts der Beträge der Vektoren mit dem Kosinus des Winkels, den sie bilden, d. h.
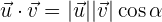
Die gebräuchlichste Art, das Punktprodukt zu definieren, ist jedoch nicht diese, sondern die Summe der Produkte ihrer jeweiligen Koordinaten, d. h, wenn 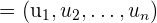 und
und  , können wir das Punktprodukt wie folgt definieren
, können wir das Punktprodukt wie folgt definieren
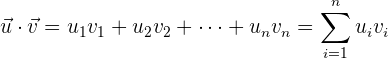
Beispiel
Bestimme das Punktprodukt der zwei Vektoren mit den folgenden Koordinaten:

Wir wenden die Definition an und erhalten
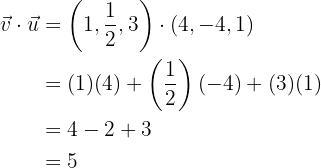
Eigenschaften des Punktprodukts
Für das Punktprodukt gelten die folgenden Regeln:
1 Kommutativgesetz.
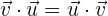
2 Assoziativgesetz in Verbindung mit reellen Zahlen.

3 Distributivgesetz.
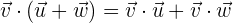
4 Wenn  , gilt
, gilt
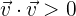
Betrag eines Vektors in Bezug auf das Punktprodukt
Wir können den Betrag eines Vektors durch das Punktprodukt ausdrücken, indem wir beachten, dass
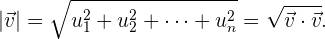
Einfach ausgedrückt ist der Betrag eines Vektors die Wurzel aus dem Punktprodukt des Vektors mit sich selbst.
Beispiel
Wir berechnen den Betrag des folgenden Vektors

Wir wenden die vorher genannte Regel an und erhalten
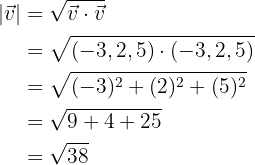
Winkel zwischen zwei Vektoren in Bezug auf das Punktprodukt
Wir können den Winkel zwischen zwei Vektoren als ihr Punktprodukt definieren. Zunächst beachten wir, dass der Kosinus des Winkels, den die zwei Vektoren  und
und  bilden, gegeben ist durch
bilden, gegeben ist durch
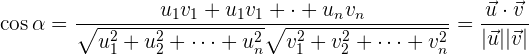
Sobald wir den Kosinus haben, können wir den Winkel berechnen, indem wir einfach die trigonometrische Umkehrfunktion Arkuskosinus anwenden, also
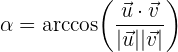
Beispiel
Wir berechnen den Winkel, den die Vektoren bilden

Mit der vorhergehenden Formel erhalten wir

Orthogonale Vektoren
Zwei Vektoren  und
und  sind zueinander orthogonal, wenn ihr Punktprodukt null (gleich
sind zueinander orthogonal, wenn ihr Punktprodukt null (gleich  ) ist. Wenn also gilt, dass
) ist. Wenn also gilt, dass
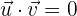
Es ist also zu beachten, dass die Orthogonalität durch das Punktprodukt definiert ist.
Beispiel
Beweise, dass die Vektoren

zueinander orthogonal sind.
Wir berechnen das Punktprodukt der Vektoren
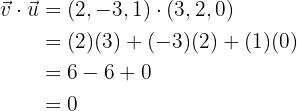
Da das Punktprodukt  ist, sind die Vektoren zueinander orthogonal.
ist, sind die Vektoren zueinander orthogonal.
Geometrische Interpretation des Punktprodukts
Das Punktprodukt zweier Vektoren, die nicht null sind (außer dem Nullvektor), ist gleich dem Betrag des einen Vektors mal dem Betrag der Projektion des anderen Vektors auf ihn. Wir sehen uns folgende Abbildung an
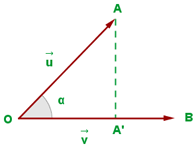
Wir stellen fest, dass 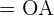 ,
, 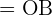 und
und 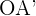 die Projektion von
die Projektion von  auf
auf  ist. Somit gilt:
ist. Somit gilt:
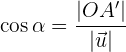
Wie wir jedoch bereits gesehen haben, ist der Kosinus ebenfalls gegeben durch
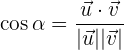
Wir setzen gleich und erhalten
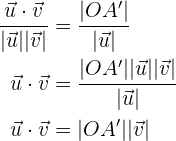
Wie gegeben, wird die skalare Projektion von  auf
auf  mit der folgenden Formel berechnet
mit der folgenden Formel berechnet
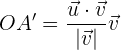
Es ist klar, dass wir einen Einheitsvektor mit der Richtung  erhalten und ihm dann eine Länge gleich
erhalten und ihm dann eine Länge gleich  zuweisen.
zuweisen.
Aufgaben
Die folgenden Übungsaufgaben dienen dazu, das Punktprodukt und seine Eigenschaften besser zu verstehen.
Gegeben sind die Vektoren

Berechne ihre Beträge.
Wir berechnen die Beträge
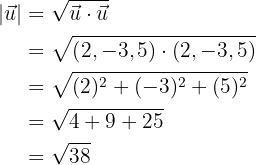
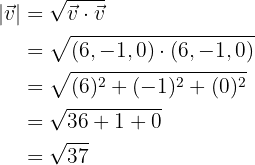
Gegeben sind die Vektoren

Berechne das Skalarprodukt.
Wir berechnen das Skalarprodukt
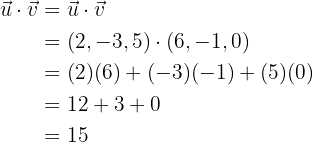
Gegeben sind die Vektoren

Berechne den Winkel, den sie bilden.
Wir wenden die uns bereits bekannte Formel an und nutzen den Arkuskosinus
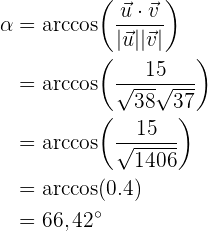
Gegeben sind die Vektoren

Bestimme den Wert für  , sodass die Vektoren zueinander orthogonal sind.
, sodass die Vektoren zueinander orthogonal sind.
Damit zwei Vektoren zueinander orthogonal sind, muss ihr Punktprodukt gleich null sein, also
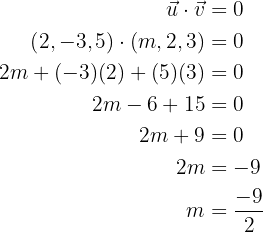
Mit KI zusammenfassen:













