Kapitel
Ein dreidimensionales Koordinatensystem wird durch Einzeichnen einer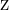 
-Achse konstruiert, die im Koordinatenursprung senkrecht zu den Achsen 
und 
steht.
Jeder Punkt ist durch drei Koordinaten gegeben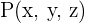 
.
Die Koordinatenachsen bestimmen drei Koordinatenebenen: 
und 
. Diese Koordinatenebenen unterteilen den Raum in 8 Bereiche, die Oktanten genannt werden, wobei im 1. Oktanten alle drei Koordinaten positiv sind.
Vektor im Raum
Ein Vektor im Raum hat seinen Ausgangspunkt an einem Punkt und seine Spitze an einem anderen Punkt.
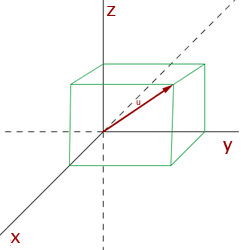
Komponenten eines Vektors im Raum
Die Koordinaten von 
und 
sind: 
und 
Die Koordinaten oder Komponenten des Vektors 
sind die Koordinaten der Spitze minus die Koordinaten des Ausgangspunktes.
Beispiel:
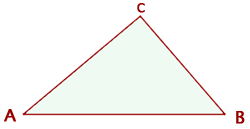
Bestimme die Komponenten der Vektoren, die im Dreieck mit den Eckpunkten 
y 
gezeichnet werden können.
Betrag eines Vektors
Der Betrag eines Vektors ist die Länge der gerichteten Strecke, die ihn definiert.
Der Betrag eines Vektors ist immer eine positive Zahl und nur der Nullvektor hat einen Betrag von 0.
Berechnung des Betrags, wenn die Komponenten bekannt sind
Der Betrag eines Vektors 
ist
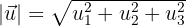
Beispiel:
Gegeben sind die Vektoren 
und 
. Berechne die Beträge von 
und 
·
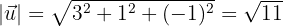
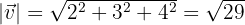
Berechnung des Betrags, wenn die Koordinatenpunkte bekannt sind
Der Betrag eines Vektors mit den Ausgangspunkten und Endpunkten 
ist
Distanz zwischen zwei Punkten
Die Distanz zwischen zwei Punkten ist gleich dem Betrag des Vektors, der diese Punkte als Ausgangs- und Endpunkte hat.
Beispiel:
Berechne die Distanz zwischen den Punkten 
und 
.
Einheitsvektor
Ein Einheitsvektor hat einen einheitlichen Betrag.
Die Normierung eines Vektors besteht darin, ihm einen anderen Einheitsvektor zuzuordnen, der dieselbe Richtung und dieselbe Orientierung wie der gegebene Vektor hat und den man erhält, indem man jede Komponente des Vektors durch ihren Betrag dividiert.
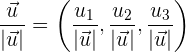
Addition von Vektoren
Um zwei Vektoren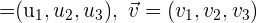 
zu addieren, werden ihre jeweiligen Komponenten addiert
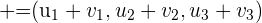
Beispiel:
1 Gegeben sind 
. Bestimme den Vektor 
.
2 Gegeben sind die Vektoren 
und . Berechne den Betrag des Vektors 
.
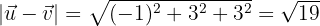
Regeln zur Addition von Vektoren
Assoziativ
Kommutativ
Neutrales Element
Gegenzahl
Produkt aus reeller Zahl und Vektor
Das Produkt aus einer reellen Zahl 
und einem Vektor ergibt einen weiteren Vektor:
Mit derselben Richtung wie der Vektor .
Mit derselben Orientierung wie der Vektor , wenn 
positiv ist.
Von entgegengesetzter Orientierung des Vektors , wenn negativ ist.
Mit dem Betrag 
Die Komponenten des resultierenden Vektors erhält man durch Multiplikation der Komponenten des Vektors mit .
Rechenregeln zum Produkt aus einer Zahl und einem Vektor
Assoziativ
Distributiv in Bezug auf die Addition von Vektoren
Distributiv in Bezug auf Skalare
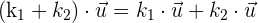
Neutrales Element
Beispiel:
Gegeben ist 
. Bestimme so, dass 
.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
