Kapitel
Nachdem wir nun die Definition eines Vektors kennen, werden wir einige der grundlegenden Rechenoperationen untersuchen, die zwischen Vektoren durchgeführt werden können.
Vektoraddition
Wenn wir zwei Vektoren 
und 
haben, ist die Summe aus 
und 
Der Summenvektor und ist also der Vektor, den man erhält, wenn man die jeweiligen Komponenten dieser Vektoren addiert: Die erste Komponente des Vektors wird mit der ersten Komponente des Vektors addiert. Die zweite Komponente des Vektors wird mit der zweiten Komponente des Vektors addiert.
Grafische Interpretation der Addition
Die folgende Grafik stellt die Summe der Vektoren und dar:
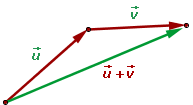
Wenn und zwei freie Vektoren sind, müssen wir, um diese grafisch zu addieren, den Repräsentanten des Vektors auswählen, dessen Anfangspunkt der Endpunkt des Vektors ist. 
ist schließlich der Vektor, dessen Anfangspunkt der Anfangspunkt des Vektors ist und dessen Endpunkt der Endpunkt des Vektors ist.
Es ist auch möglich, einen Repräsentanten des Vektors so zu wählen, dass sein Anfangspunkt der Endpunkt des Vektors ist. Die Summe ergibt das gleiche Ergebnis, aber wir erhalten Sie, indem wir den Anfanfangspunkt des Vektors mit dem Endpunkt des Vektors verbinden.
Parallelogrammgleichung
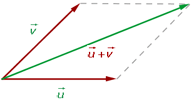
Was wir oben als grafische Summe der Vektoren besprochen haben, ist als Parallelogrammgleichung bekannt. Insbesondere wenn wir zwei freie Vektoren mit einem gemeinsamen Anfangspunkt addieren möchten, müssen wir Geraden parallel zu den Vektoren zeichnen. Auf diese Weise erhält man ein Parallelogramm, dessen Diagonale - die im Anfangspunkt der Vektoren beginnt - die Summe der Vektoren selbst ist.
Die folgende Abbildung zeigt die Parallelogrammgleichung.
Vektorsubtraktion
Die Differenz von und ist ganz einfach die Summe von und 
(das heißt, der Gegenvektor von ).
Wenn wir also die Komponenten von und betrachten, ist die Differenz gegeben durch
Grafisch dargestellt erhalten wir die Differenz von und auf gleiche Weise wie die Summe. Der einzige Unterschied besteht darin, dass wir den Gegenvektor von addieren. Wenn wir uns die folgende Abbildung, die 
darstellt, ansehen, stellen wir fest, dass sich im Endpunkt des Vektors der Anfangspunkt von 
befindet.
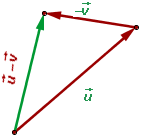
Wir stellen fest, dass die Differenz grafisch dargestellt der Vektor ist, der den Endpunkt des Vektors mit dem Endpunkt des Vektors verbindet.
Skalarmultiplikation
Die Multiplikation eines Vektors mit einer Zahl 
wird 
oder 
geschrieben. Die Zahl nennt man auch Skalar. Außerdem ergibt die Multiplikation mit einem Skalar einen weiteren Vektor, der folgende Eigenschaften besitzt:
- hat die gleiche Richtung wie .
- Wenn positiv ist, hat die gleiche Orientierung wie .
- Wenn negativ ist, hat die entgegengesetzte Orientierung wie .
- Der Betrag von ist
Die folgende Grafik zeigt die Multiplikation von mit 3.
Wenn , ist die Multiplikation mit einem Skalar gegeben durch
Beispielaufgaben zum Rechnen mit Vektoren
Wir sehen uns die Vektoren 
und 
an. Somit:
1 Die Summe ist gegeben durch:
2 Die Differenz ist:
3 Der Gegenvektor von ist:
4 Die Skalarmultiplikation aus und 3 ist gegeben durch:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
