Kapitel
Definition von Maximum und Minimum
Wenn 
in 
ableitbar ist, ist ein relatives oder lokales Extremum, wenn:
1 
.
2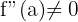 
.
Lokale Maxima
Wenn und 
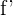in ableitbar sind, ist ein relatives oder lokales Maximum, wenn gilt:
1
2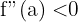 
Lokale Minima
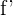Wenn und in ableitbar sind, ist ein relatives oder lokales Minimum, wenn gilt:
1
2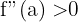 
Berechnung von Maxima und Minima
Para encontrar los extremos relativos o locales de una función 
, realizaremos lo siguiente:
1 Ermittle die erste Ableitung 
sowie ihre Nullstellen.
2 Berechne die zweite Ableitung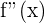
und ermittele die Werte, die die Nullstellen der ersten Ableitung in 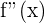annehmen. Bestimme danach, ob es sich laut Bedingung um ein Maximum oder Minimum handelt. Beachte dabei:
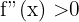Wir haben ein Minimum
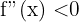Wir haben ein Maximum
3 Berechne die zweite Koordinate der relativen Extrema in der Funktion .
Beispiel für die Berechnung von Maxima und Minima
Untersuche die Maxima und Minima von:
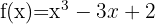
Um die lokalen Extrema zu finden, befolgen wir die oben genannten Schritte:
1 Wir berechnen die 1. Ableitung und berechnen ihre Nullstellen.
Ableitung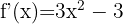 
Wir setzen die Ableitung gleich 0 und lösen
.
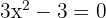
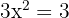
2 Wir führen die zweite Ableitung durch und berechnen das Vorzeichen, das die Nullstellen der ersten Ableitung darin annehmen, und wenn:
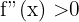Wir haben ein Minimum
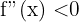Wir haben ein Maximum
Zweite Ableitung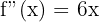 
Wenn 
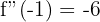Maximum
Wenn 
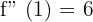Minimum
3 Wir berechnen die zweite Koordinate der relativen Extrema in der Funktion.
Maximum 
Minimum 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
