
Definition und Eigenschaften des Schwerpunkts
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der Seitenhalbierenden. In der folgenden Abbildung ist der Schwerpunkt eines Dreiecks zu sehen:
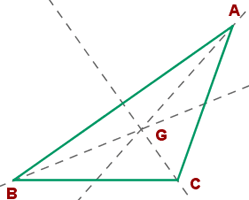
Die Koordinaten des Schwerpunkts des Dreiecks mit den Eckpunkten 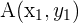 ,
, 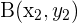 und
und 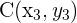 sind
sind
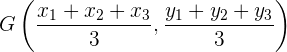
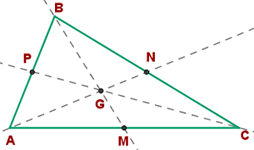
Die Seitenhalbierenden eines Dreiecks sind die Geraden, die den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt verbinden. In der folgenden Abbildung ist also der Punkt  der Mittelpunkt zwischen
der Mittelpunkt zwischen  und
und  (und etwas Ähnliches passiert mit den Punkten
(und etwas Ähnliches passiert mit den Punkten  und
und  ).
).
Nun sehen wir uns ein Dreieck im Raum an, dessen Koordinaten  ,
,  und
und  sind. In diesem Fall sind die Koordinaten des Schwerpunkts
sind. In diesem Fall sind die Koordinaten des Schwerpunkts
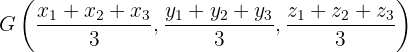
In der Geometrie werden die Begriffe Baryzentrum, Schwerpunkt und Zentroid synonym verwendet. In der Physik hängt der Begriff des Schwerpunkts jedoch von der Dichte des Objekts ab und unterscheidet sich vom Baryzentrum.
Wenn ein Objekt  aus den Punkten
aus den Punkten 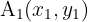 ,
,  ,
,  ,
,  gebildet wird, lauten die Koordinaten des Schwerpunkts
gebildet wird, lauten die Koordinaten des Schwerpunkts
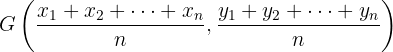
Beispiele
Ermittle die Koordinaten des Schwerpunkts für:
a ein Dreieck mit den Eckpunkten 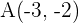 ,
, 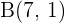 und
und  ,
,
b ein Dreieck mit den Eckpunkten  ,
,  und
und  .
.
In dieser Aufgabe brauchen wir nur die Formel für den Schwerpunkt eines Dreiecks anzuwenden. Somit:
a Für den ersten Fall haben wir

b Und für den zweiten Fall

Wir betrachten ein Dreieck, bei dem zwei seiner Eckpunkte  und
und 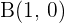 sind. Wenn der Schwerpunkt des Dreiecks
sind. Wenn der Schwerpunkt des Dreiecks  ist, wie lauten dann die Koordinaten des dritten Eckpunkts
ist, wie lauten dann die Koordinaten des dritten Eckpunkts  ?
?
Wir bezeichnen die Koordinaten von  als
als 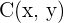 . Dann wird der Schwerpunkt wie folgt berechnet
. Dann wird der Schwerpunkt wie folgt berechnet

Wir haben allerdings auch  , weshalb
, weshalb
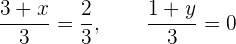
Wir multiplizieren mit 3 und erhalten

Daraus folgt, dass  und
und  . Somit ist der Eckpunkt
. Somit ist der Eckpunkt 

 ,
, 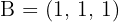 und
und  sind die Eckpunkte eines Dreiecks im Raum. Ermittle die Koordinaten des Schwerpunkts.
sind die Eckpunkte eines Dreiecks im Raum. Ermittle die Koordinaten des Schwerpunkts.
Wir verwenden einfach die Formel für die Koordinaten des Schwerpunkts:

4 Gegeben ist das Dreieck mit den Eckpunkten 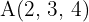 ,
, 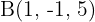 und
und  . Bestimme:
. Bestimme:
a Die Gleichungen der Seitenhalbierenden des Dreiecks
b Die Koordinaten des Schwerpunkts des Dreiecks
c Die Koordinaten des Schwerpunkts des Dreiecks, dessen Eckpunkte die Mittelpunkte der Seiten des Dreiecks  sind.
sind.
Sieh dir folgende Abbildung an:
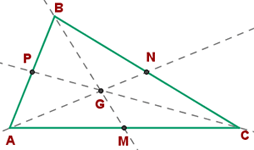
a Der erste Schritt besteht darin, die Koordinaten der Punkte  ,
,  und
und  zu berechnen. Man beachte, dass
zu berechnen. Man beachte, dass  der Mittelpunkt von
der Mittelpunkt von  und
und  ist. Das heißt
ist. Das heißt

Analog dazu ist  der Mittelpunkt von
der Mittelpunkt von  und
und 
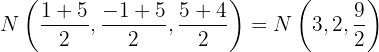
Der Punkt  ist der Mittelpunkt von
ist der Mittelpunkt von  und
und 

Wir haben also bereits die Mittelpunkte und können die Gleichungen der Geraden berechnen. Da wir Geraden im Raum haben, ist die Gleichung der Geraden die Gleichung in Parameterform. Wenn  und
und  zwei Punkte im Raum sind, dann lautet die Gleichung der Geraden durch
zwei Punkte im Raum sind, dann lautet die Gleichung der Geraden durch  und
und 
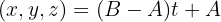
Somit ist die Seitenhalbierende, die durch  und
und 
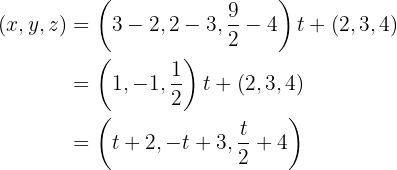
Das heißt
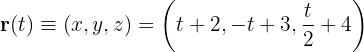
Die Seitenhalbierende, die durch  und
und  verläuft, ist
verläuft, ist
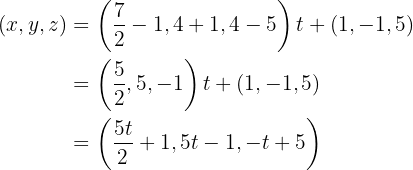
Das heißt

Und schließlich ist die Seitenhalbierende, die durch  und
und  verläuft
verläuft
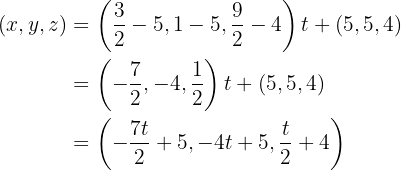
Das heißt
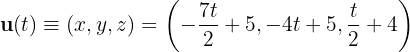
b Um die Koordinaten des Schwerpunkts zu berechnen, haben wir zwei Möglichkeiten: den Schnittpunkt der drei Seitenhalbierenden zu finden oder die Formel zu verwenden, die wir bereits kennen. Da es einfacher ist, die Formel zu verwenden, tun wir genau das:
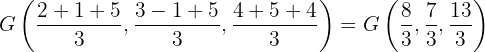
c Nun berechnen wir den Schwerpunkt des Dreiecks 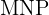 . Wir verwenden die gleiche Formel
. Wir verwenden die gleiche Formel

Wir stellen fest, dass beide Dreiecke den gleichen Schwerpunkt haben.












