Kapitel
In der karthesischen Ebene ist das Skalarprodukt — auch Punktprodukt oder inneres Produkt genannt — aus zwei Vektoren  und
und 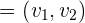 eine positive reelle Zahl, die dem Produkt aus ihren Beträgen und dem Kosinus des Winkels
eine positive reelle Zahl, die dem Produkt aus ihren Beträgen und dem Kosinus des Winkels  , den sie bilden, entspricht
, den sie bilden, entspricht
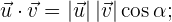
und in seiner analytischen Darstellung ist es äquivalent zur Summe des Produkts seiner koordinatenweisen Einträge:
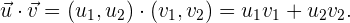
Im kartesischen Raum entspricht die geometrische Interpretation des Skalarprodukts dem Winkel  , der in der Ebene gebildet wird, die die Vektoren enthält. Darüber hinaus wird der Betrag eines jeden Vektors auf die gleiche Weise berechnet, jedoch unter Berücksichtigung einer weiteren Koordinate. Der Betrag eines Vektors wird auch als Norm bezeichnet:
, der in der Ebene gebildet wird, die die Vektoren enthält. Darüber hinaus wird der Betrag eines jeden Vektors auf die gleiche Weise berechnet, jedoch unter Berücksichtigung einer weiteren Koordinate. Der Betrag eines Vektors wird auch als Norm bezeichnet:
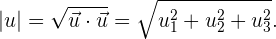
Zum Beispiel ist der Betrag des Vektors 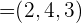


Formeln für Skalarprodukte im Raum
Das Skalarprodukt für zwei Vektoren 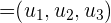 und
und 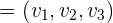 im karthesischen Raum ist gegeben durch
im karthesischen Raum ist gegeben durch
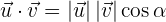
und seine analytische Darstellung als

Und der Winkel  als
als
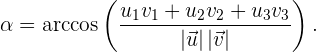
Beispiel:
1 Ermittle das Skalarprodukt der Vektoren 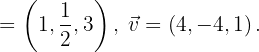
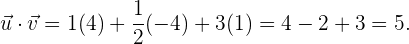
2 Berechne die Beträge der Vektoren 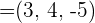 und
und 
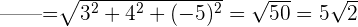

3 Ermittle den Winkel, den die Vektoren 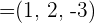 und
und 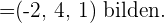
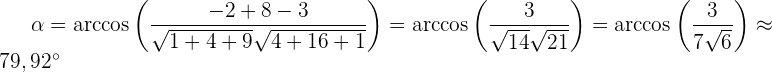
Verallgemeinerungen des Skalarprodukts im Raum
Orthogonale Vektoren
Wie in der kartesischen Ebene sind zwei Vektoren orthogonal, wenn ihr Skalarprodukt gleich 0 ist. Somit ist 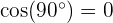 . Also sind die Vektoren
. Also sind die Vektoren  und
und  orthogonal
orthogonal
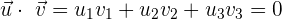
Aufgabe:
Berechne die Werte für  , sodass der Vektor
, sodass der Vektor  orthogonal zu den Vektoren
orthogonal zu den Vektoren 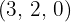 und
und 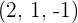 ist.
ist.

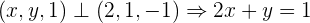
Und somit ist 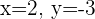 .
.
Anmerkung: Wenn die Vektoren  und
und  parallel sind, beträgt der entstehende Winkel
parallel sind, beträgt der entstehende Winkel 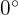 . Somit ist
. Somit ist 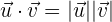 und
und  .
.
Anmerkung: Wenn die Vektoren  und
und  einen Winkel von
einen Winkel von 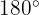 bilden, ist
bilden, ist 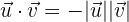 . Somit ist
. Somit ist 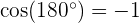 .
.
Rechengesetze für das Skalarprodukt
1 Kommutativ.
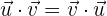
2 Assoziativ hinsichtlich der Multiplikation mit einem Skalar.

3 Distributiv hinsichtlich der Summe der Vektoren.

4 Da der Vektor ungleich 0 ist, ist das Skalarprodukt immer größer als 0.

Geometrische Interpretation des Skalarprodukts
Bei zwei Vektoren und der Betrachtung der Ebene, in der sie liegen, kann das Skalarprodukt als das Produkt des Moduls des einen Vektors mit dem Modul der Abbildung des anderen Vektors auf ihn interpretiert werden. Bei zwei Vektoren und der Betrachtung der Ebene, in der sie liegen, kann das Skalarprodukt als das Produkt aus dem Betrag des einen Vektors und dem Betrag der Abbildung des anderen Vektors auf diesen interpretiert werden.

Da 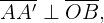 wenden wir die trigonometrischen Funktionen an
wenden wir die trigonometrischen Funktionen an
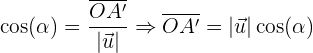

Somit ist  die Abbildung des Vektors
die Abbildung des Vektors  auf den Vektor
auf den Vektor 
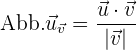
und die Vektorprojektion von  auf
auf  von einem Vektor mit dem Betrag der Einheit parallel zu
von einem Vektor mit dem Betrag der Einheit parallel zu  :
:
Aufgabe:
Gegeben sind die Vektoren 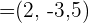 und
und  . Berechne:
. Berechne:
a) Die Beträge von 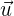 und
und  .
.

b) Das Skalarprodukt von 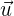 und
und  .
.
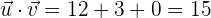
c) Den Winkel  , den sie bilden.
, den sie bilden.
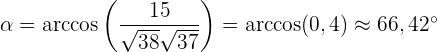
d) Die Abbildung von 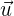 auf
auf  .
.
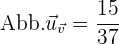
e) Die Abbildung von  auf
auf  .
.
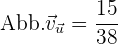
f) Berechne den Wert von  , sodass die Vektoren
, sodass die Vektoren 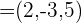 und
und 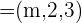 zueinander orthogonal sind.
zueinander orthogonal sind.
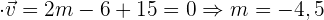
Richtungskosinus einer Orthonormalbasis
In einer Orthonormalbasis sind die Richtungskosinus des Vektors 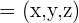 die Kosinus der Winkel, die
die Kosinus der Winkel, die  mit jedem der Vektoren der Basis bildet.Betrachtet man beispielsweise die Standardbasis
mit jedem der Vektoren der Basis bildet.Betrachtet man beispielsweise die Standardbasis  , so ergibt sich:
, so ergibt sich:
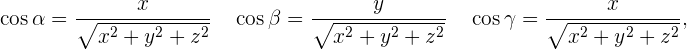 ,
,
wobei gilt, dass
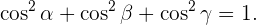
Aufgabe:
Bestimme die Richtungskosinus des Vektors  hinsichtlich der Standardbasis und zeige, dass ihre Summe 1 ist.
hinsichtlich der Standardbasis und zeige, dass ihre Summe 1 ist.


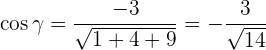
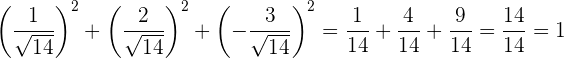
Mit KI zusammenfassen:












