Ungleichungen mit einer Variabel
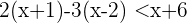
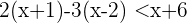
1 Wir lösen die Klammern auf, indem wir die erste mit  und die zweite mit
und die zweite mit  multiplizieren:
multiplizieren:
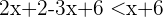
2 Wir gruppieren die Variablen auf einer Seite der Ungleichung
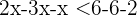
3 Wir teilen durch  und wechseln die Richtung der Ungleichung
und wechseln die Richtung der Ungleichung


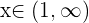
Ungleichungen mit einer Variabel
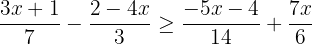
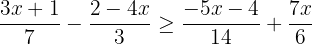
1 Wir finden das kleinste gemeinsame Vielfache der Nenner, um die Nenner zu entfernen
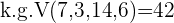
 wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert
wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert
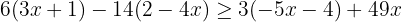
2 Wir lösen die Klammern auf, indem wir die erste mit  , die zweite mit
, die zweite mit 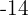 und die dritte mit
und die dritte mit  multiplizieren:
multiplizieren:

3 Wir gruppieren die Variablen auf einer Seite der Ungleichung
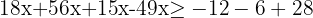
4 Wir rechnen die gleichen Variablen zusammen
5 Wir vereinfachen indem wir durch  teilen
teilen
6 Wir teilen auf beiden Seiten durch 
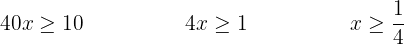

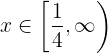
Ungleichungen mit einer Variabel
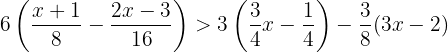
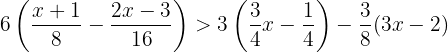
1 Wir lösen die Klammern auf, indem wir die erste mit  , die zweite mit
, die zweite mit  und die dritte mit
und die dritte mit 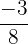 multiplizieren:
multiplizieren:
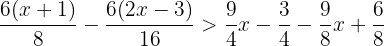
2 Wir finden das kleinste gemeinsame Vielfache der Nenner, um die Nenner zu entfernen
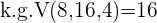
 wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert
wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert
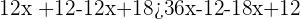
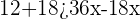
3 Wir gruppieren die Variablen auf einer Seite, vereinfachen indem wir durch  teilen und teilen beide Seiten durch
teilen und teilen beide Seiten durch  .
.
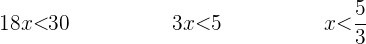
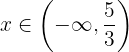
Ungleichungen mit einer Variabel
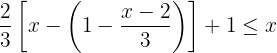
Die Ungleichung lösen:
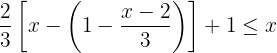
1 Wir entfernen die Klammer, indem wir mit  multiplizieren, so dass die eckige Klammer zu einer Klammer wird.
multiplizieren, so dass die eckige Klammer zu einer Klammer wird.
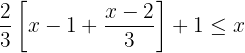
2 Wir lösen die Klammer auf, indem wir mit  multiplizieren
multiplizieren
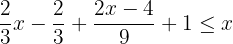
3 Wir finden das kleinste gemeinsame Vielfache, um die Nenner zu entfernen.
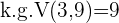
 wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert.
wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert.

4 Wir gruppieren die gleichen Begriffe auf einer Seite der Gleichung und führen die aufgezeigten Additionen und Subtraktionen durch.
Da der Koeffizient von  negativ ist, multiplizieren wir mit
negativ ist, multiplizieren wir mit  , wodurch sich die Richtung der Ungleichung ändert.
, wodurch sich die Richtung der Ungleichung ändert.


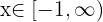
Ungleichungen mit einer Variabel
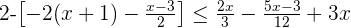
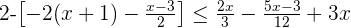
1 Eckige Klammern auflösen
Wir lösen die Klammer auf, indem wir mit  multiplizieren, so dass die eckige Klammer zu einer Klammer wird:
multiplizieren, so dass die eckige Klammer zu einer Klammer wird:
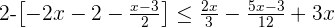
2 Klammer auflösen.
Wir lösen die Klammer auf, indem wir mit  multiplizieren:
multiplizieren:
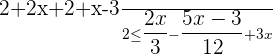
3 Nenner entfernen.
Wir finden das kleinste gemeinsame Vielfache:
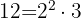
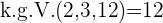
 wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert.
wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert.
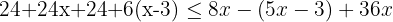
Wir lösen die Klammer auf, indem wir die erste mit  und die zweite mit
und die zweite mit  multiplizieren:
multiplizieren:

4 Wir gruppieren die Variablen  auf einer Seite der Ungleichung.
auf einer Seite der Ungleichung.

5 Wir rechnen aus
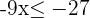
6 Wenn der Koeffizient von  negativ ist, multiplizieren wir mit
negativ ist, multiplizieren wir mit  , wodurch sich die Richtung der Ungleichung ändert.
, wodurch sich die Richtung der Ungleichung ändert.
Diesen Schritt führen wir immer durch, bevor wir die Unbekannte isolieren

7 Wir isolieren die Unbekannte, indem wir beide Seiten durch  teilen.
teilen.

In der Praxis sagt man oft, dass  multipliziert und auf die andere Seite der Ungleichung übergeht, wo es
multipliziert und auf die andere Seite der Ungleichung übergeht, wo es  dividiert.
dividiert.

Wir erhalten die Lösung in Form einer Ungleichung, aber wir können sie auch folgendermaßen ausdrücken:
Graphisch
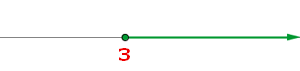
Als Intervall ausgedrückt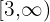
Berechne den angegebenen Wert
Finde die Werte von  , für welche die Wurzeln der Gleichung
, für welche die Wurzeln der Gleichung 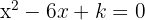 sowohl reell als auch verschieden sind.
sowohl reell als auch verschieden sind.
Damit die Gleichung zwei reelle und verschiedene Wurzeln hat, muss die Diskriminante 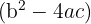 größer als Null sein.
größer als Null sein.
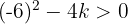
Wir lösen die Ungleichung:
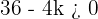
Wir multiplizieren mit  und ändern das Vorzeichen der Ungleichung.
und ändern das Vorzeichen der Ungleichung.


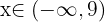
Ungleichungen mit zwei Variablen


1 Wir wandeln die Ungleichung in eine Gleichung um.

2 Wir geben der Variablen x zwei Werte, wodurch wir zwei Punkte erhalten.


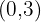


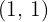
3 Durch die Darstellung und Verbindung dieser Punkte erhalten wir eine Gerade.
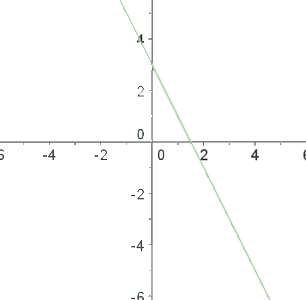
Wir nehmen den Punkt  und setzen ihn in die Ungleichung ein.
und setzen ihn in die Ungleichung ein.

Da die Ungleichung erfüllt ist, ist die Lösung die Halbebene, in der sich  befindet, einschließlich der Geraden, da wir die kleineren und auch die gleichen Punkte nehmen.
befindet, einschließlich der Geraden, da wir die kleineren und auch die gleichen Punkte nehmen.
In diesem Fall zeichnen wir die Gerade mit einer durchgehenden Linie.
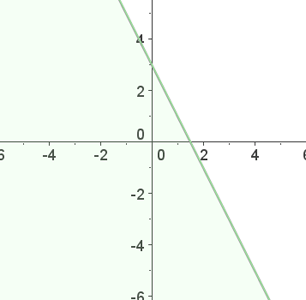
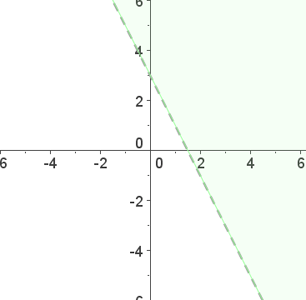
Ungleichungen mit zwei Variablen
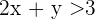
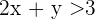
1 Wir wandeln die Ungleichung in eine Gleichung um.

2 Wir geben der Variablen  zwei Werte, wodurch wir zwei Punkte erhalten.
zwei Werte, wodurch wir zwei Punkte erhalten.


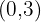


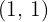
3 Durch Darstellung und Verbindung dieser Punkte erhalten wir eine Gerade.
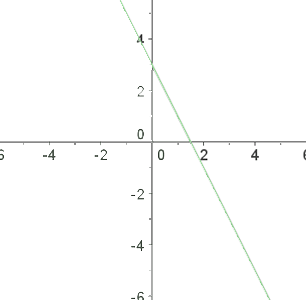
Wir nehmen den Punkt  und setzen ihn in die Ungleichung ein.
und setzen ihn in die Ungleichung ein.

Da die Ungleichung nicht erfüllt ist, ist die Lösung die Halbebene, in der sich  nicht befindet
nicht befindet
In diesem Fall (größer als, aber nicht gleich) gehören die Punkte auf der Geraden nicht zur Lösung.
In diesem Fall zeichnen wir die Gerade mit gestrichelten Linien