Kapitel
Ein System von Ungleichungen mit zwei Unbekannten hat als Lösung eine der Halbebenen, die sich aus der Darstellung der resultierenden Gleichung ergeben, die du durch Umformung der Ungleichung in eine Gleichheit erhältst.
Schritte zum Lösen linearer Ungleichungen mit zwei Unbekannten
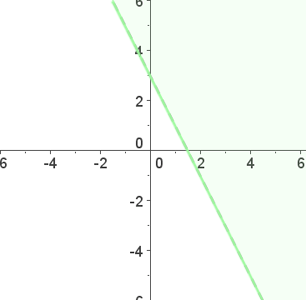
Löse die Ungleichung: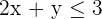 
1 Verwandle Ungleichheit in Gleichheit.
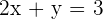
2 Gebe einer der beiden Variablen zwei Werte, also erhältst du zwei Punkte.
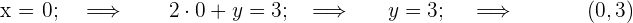
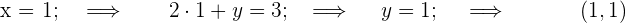
3 Wenn du diese Punkte darstellst und verbindest, erhältst du eine Gerade.
4 Nimm wieder einen Punkt, zum Beispiel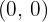 
, und setze ihn in die Ungleichung ein. Wenn dies zutrifft, ist die Lösung die Halbebene, auf der sich der Punkt befindet, andernfalls ist die Lösung die andere Halbebene.
Mögliche Fälle von Ungleichungen
Kleiner oder gleich
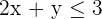
Nimm den Punkt 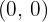und setze ihn in die Ungleichung ein.
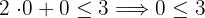
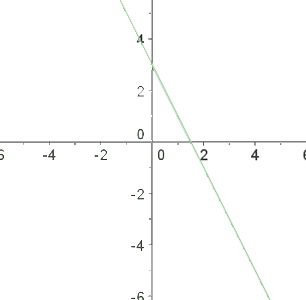
Da die Ungleichung erfüllt ist, ist die Lösung die Halbebene, in der sich 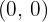, befindet, einschließlich der Geraden, da wir du Nebenpunkte und auch die Gleichpunkte verwendest
In diesem Fall zeichnest du eine durchgehende Gerade
Kleiner
Nimm den Punkt 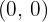und setze ihn in die Ungleichung ein.
Da sie erfüllt ist, ist die Lösung die Halbebene, in der sich 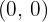befindet
In diesem Fall (kleiner als, aber nicht gleich) gehören die Punkte auf der Geraden nicht zur Lösung
In diesem Fall ziehst du eine gestrichelte Gerade
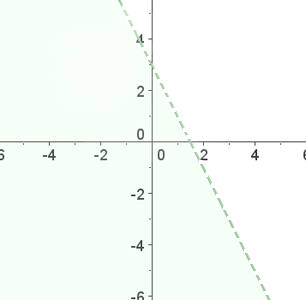
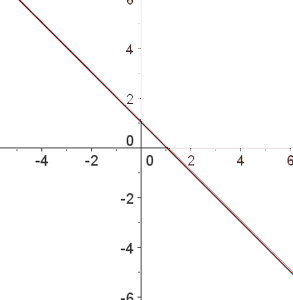
Größer
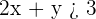
Nimm den Punkt 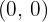und setze ihn in die Ungleichung ein.
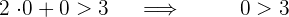No
Da die Ungleichung nicht erfüllt ist, ist die Lösung die Halbebene, in der 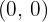nicht gefunden wird
In diesem Fall (größer als, aber nicht gleich) gehören die Punkte auf der Geraden nicht zur Lösung.
In diesem Fall ziehst du eine gestrichelte Gerade
Größer oder gleich
Nimm den Punkt 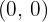und setze ihn in die Ungleichung ein.
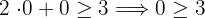No
Da die Ungleichung nicht erfüllt ist, ist die Lösung die Halbebene, in der 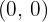nicht gefunden wird
In diesem Fall (größer oder gleich) gehören die Punkte auf der Geraden zur Lösung.
In diesem Fall zeichnest du eine durchgehende Gerade
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
