Bei Ungleichungssystemen mit einer Unbekannten wird jede Ungleichung einzeln gelöst, wobei die Lösung des Systems die Schnittmenge der Lösungsmengen aller Ungleichungen ist.
Beispiele
1
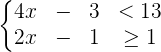
Löse die linearen Ungleichungen
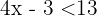
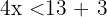
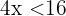
Teile beide Seiten der Ungleichung durch  und erhalte
und erhalte

Löse die zweite Ungleichung
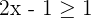
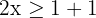

Teile beide Seiten der Ungleichung durch  und erhalte
und erhalte
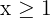
Stelle die Lösungen grafisch dar

Die Lösung ist die Schnittmenge der Ungleichungslösungen, d. h. alle Punkte, die mit beiden übereinstimmen:
x ∈ [1, 4)
2
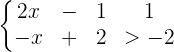
Löse die linearen Ungleichungen und beginne mit der ersten
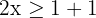

Teile beide Seiten der Ungleichung duch  und du erhältst
und du erhältst
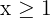
Wiederhole diese Schritte mit der zweiten Ungleichung:
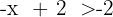
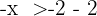
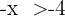
Teile beide Seiten der Ungleichung durch  und mache einen Vorzeichenwechsel
und mache einen Vorzeichenwechsel
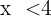
Stelle die Lösungen grafisch dar
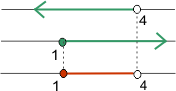
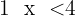
x ∈ [1, 4)
3

Löse die linearen Ungleichungen
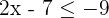

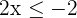


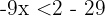
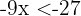
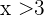
Stelle die Lösungen grafisch dar

Du stellst fest, dass es keine gemeinsamen Punkte gibt. Daher ist die Schnittstelle der Lösunsmengen ∅
Es gibt keine Lösung.



