Drücke den Vektor 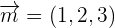 als Linearkombination der folgenden Vektoren aus:
als Linearkombination der folgenden Vektoren aus: 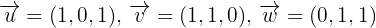 .
.
Drücke den Vektor 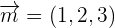 als Linearkombination der folgenden Vektoren aus:
als Linearkombination der folgenden Vektoren aus: 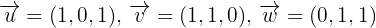 .
.
1 Wir drücken den Vektor 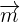 als Linearkombination von
als Linearkombination von 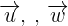 aus
aus
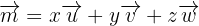 .
.
2 Wir setzen die Werte der Vektoren ein
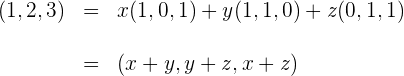
3 Wir erhalten das Gleichungssystem
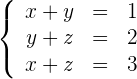
4 Wir addieren die drei Gleichungen Glied für Glied, vereinfachen die erhaltene Gleichung und subtrahieren jede der Gleichungen.
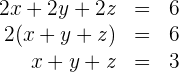
5 Wir subtrahieren jede der drei Gleichungen von der erhaltenen Gleichung und erhalten
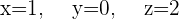
6 Die Linearkombination lautet
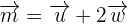
Gegeben sind 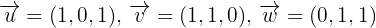 . Zeige, dass diese Vektoren linear unabhängig sind und drücke den Vektor
. Zeige, dass diese Vektoren linear unabhängig sind und drücke den Vektor 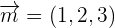 als Linearkombination dieser Vektoren aus.
als Linearkombination dieser Vektoren aus.
Gegeben sind 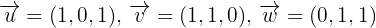 . Zeige, dass diese Vektoren linear unabhängig sind und drücke den Vektor
. Zeige, dass diese Vektoren linear unabhängig sind und drücke den Vektor 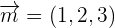 als Linearkombination dieser Vektoren aus.
als Linearkombination dieser Vektoren aus.
1Wir berechnen die Determinante von 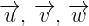
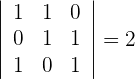
Da die Determinante ungleich 0 ist, sind 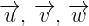 linear unabhängig.
linear unabhängig.
2 Wir drücken 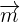 als Linearkombination von
als Linearkombination von 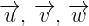 aus
aus
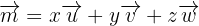 .
.
3 Wir setzen die Werte der Vektoren ein
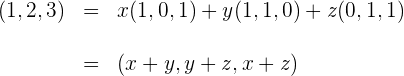
4 Wir erhalten das Gleichungssystem
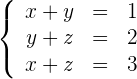
5 Wir addieren die drei Gleichungen Glied für Glied, vereinfachen die erhaltene Gleichung und subtrahieren jede der Gleichungen.
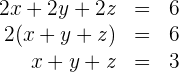
6 Wir subtrahieren jede der drei Gleichungen von der erhaltenen Gleichung und erhalten
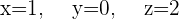
7 Die Linearkombination lautet
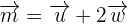
Gegeben sind die Vektoren 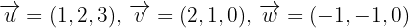 . Zeige, dass diese Vektoren eine Basis bilden und berechne die Koordinaten des Vektors
. Zeige, dass diese Vektoren eine Basis bilden und berechne die Koordinaten des Vektors  in Bezug auf diese Basis.
in Bezug auf diese Basis.
Gegeben sind die Vektoren 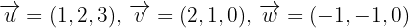 . Zeige, dass diese Vektoren eine Basis bilden und berechne die Koordinaten des Vektors
. Zeige, dass diese Vektoren eine Basis bilden und berechne die Koordinaten des Vektors  in Bezug auf diese Basis.
in Bezug auf diese Basis.
1Wir berechnen die Determinante von 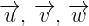
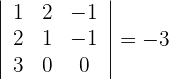
Da die Determinante ungleich 0 ist, sind 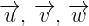 linear unabhängig und bilden eine Basis.
linear unabhängig und bilden eine Basis.
2 Wir drücken den Vektor 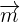 als Linearkombination von
als Linearkombination von 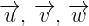 aus
aus
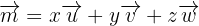 .
.
3 Wir setzen die Werte der Vektoren ein
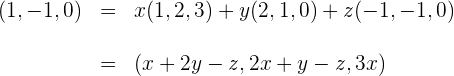
4 Wir erhalten das Gleichungssystem
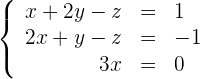
5 Wir lösen das Gleichungssystem und erhalten

6 Die Linearkombination lautet
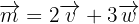
Gegeben sind die Vektoren:  . Zeige, dass sie eine Basis bilden und berechne die Koordinaten der Vektoren der Standardbasis in Bezug auf diese Basis.
. Zeige, dass sie eine Basis bilden und berechne die Koordinaten der Vektoren der Standardbasis in Bezug auf diese Basis.
Gegeben sind die Vektoren:  . Zeige, dass sie eine Basis bilden und berechne die Koordinaten der Vektoren der Standardbasis in Bezug auf diese Basis.
. Zeige, dass sie eine Basis bilden und berechne die Koordinaten der Vektoren der Standardbasis in Bezug auf diese Basis.
1Wir berechnen die Determinante von 
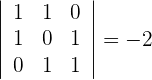
Da die Determinante ungleich 0 ist, sind  linear unabhängig und bilden eine Basis.
linear unabhängig und bilden eine Basis.
2 Wir drücken den Einheitsvektor 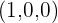 als Linearkombination von
als Linearkombination von  aus
aus
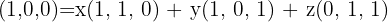 .
.
3 Wir erhalten das Gleichungssystem
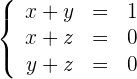
4 Wir lösen das Gleichungssystem und erhalten
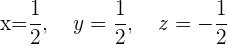
5 Die Koordinaten des Einheitsvektors 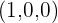 in Bezug auf die neue Basis lauten:
in Bezug auf die neue Basis lauten:

6 Wir wiederholen die Schritte 2 bis 5. Die Koordinaten der Einheitsvektoren 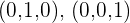 in Bezug auf die neue Basis lauten:
in Bezug auf die neue Basis lauten:

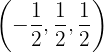
Bestimme den Wert des Parameters  , so dass die Vektoren
, so dass die Vektoren 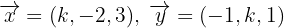 orthogonal sind:
orthogonal sind:
Bestimme den Wert des Parameters  , so dass die Vektoren
, so dass die Vektoren 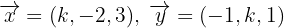 orthogonal sind:
orthogonal sind:
1Damit Vektoren orthogonal sind, muss ihr Skalarprodukt gleich 0 sein.
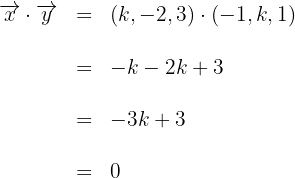
2Das Ergebnis der Gleichung 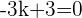 ist
ist 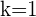 , unser gesuchter Wert.
, unser gesuchter Wert.
Gegeben sind die Punkte 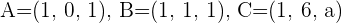 . Berechne die Werte von los valores de
. Berechne die Werte von los valores de  , so dass sich die Punkte auf einer Geraden befinden. Wie lauten die Werte von
, so dass sich die Punkte auf einer Geraden befinden. Wie lauten die Werte von  , wenn die Punkte drei Eckpunkte eines Parallelogramms mit der Fläche 3 sind?
, wenn die Punkte drei Eckpunkte eines Parallelogramms mit der Fläche 3 sind?
Gegeben sind die Punkte 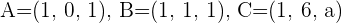 . Berechne die Werte von los valores de
. Berechne die Werte von los valores de  , so dass sich die Punkte auf einer Geraden befinden. Wie lauten die Werte von
, so dass sich die Punkte auf einer Geraden befinden. Wie lauten die Werte von  , wenn die Punkte drei Eckpunkte eines Parallelogramms mit der Fläche 3 sind?
, wenn die Punkte drei Eckpunkte eines Parallelogramms mit der Fläche 3 sind?
1Wir berechnen die Vektoren 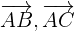

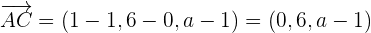
2Wenn sich 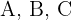 auf einer Geraden befinden, haben die Vektoren
auf einer Geraden befinden, haben die Vektoren 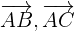 die gleiche Richtung, da sie linear unabhängig sind und ihre Elemente proportional sind
die gleiche Richtung, da sie linear unabhängig sind und ihre Elemente proportional sind

3Wir setzen die Koordinaten gleich und erhalten

4Wenn die Punkte Eckpunkte eines Parallelogramms sind, dann ist der Betrag des Vektorprodukts von 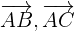 gleich dem Flächeninhalt des Parallelogramms, das auf
gleich dem Flächeninhalt des Parallelogramms, das auf 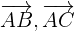 konstruiert ist.
konstruiert ist.
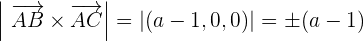
5Wir setzen die Fläche gleich 3 und erhalten


Finde zwei Vektoren, deren Betrag die Einheit ist und die orthogonal zu 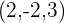 und
und 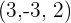 sind.
sind.
Finde zwei Vektoren, deren Betrag die Einheit ist und die orthogonal zu 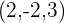 und
und 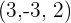 sind.
sind.
1Wir berechnen den Betrag des Vektorprodukts der beiden Vektoren

2Die orthogonalen Einheitsvektoren sind

Ermittle einen Einheitsvektor, der senkrecht zu 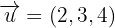 und
und 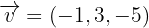 ist.
ist.
Ermittle einen Einheitsvektor, der senkrecht zu 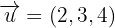 und
und 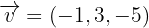 ist.
ist.
1Wir berechnen das Vektorprodukt der beiden Vektoren, das senkrecht zu 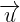 und
und 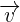 ist.
ist.
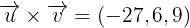
2Wir berechnen den Betrag des vorherigen Vektors
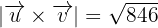
3Der Einheitsvektor ist
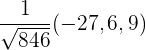
Mit KI zusammenfassen:


