Wenn 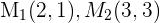 und
und 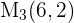 die Mittelpunkte der Seiten eines Dreiecks sind, wie lauten dann die Koordinaten der Eckpunkte des Dreiecks?
die Mittelpunkte der Seiten eines Dreiecks sind, wie lauten dann die Koordinaten der Eckpunkte des Dreiecks?
1 Wir zeichnen die Mittelpunkte und die Eckpunkte 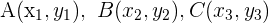 des Dreiecks ein
des Dreiecks ein
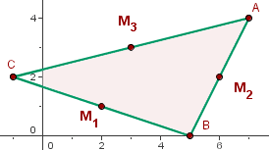
2 Aus der Mittelpunktsformel ergibt sich für die erste Koordinate
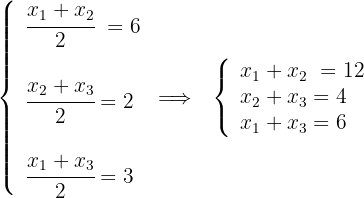
Wir subtrahieren die 2. Gleichung von der 1. Gleichung und das Ergebnis subtrahieren wir von der 3. Gleichung. Wir erhalten
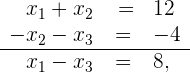
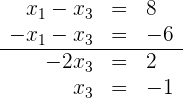
Somit ist 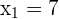 und
und 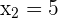
3 Aus der Mittelpunktsformel ergibt sich für die zweite Koordinate
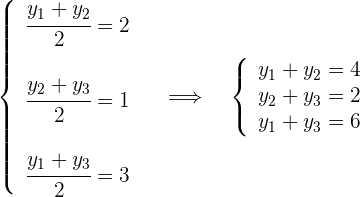
Wir subtrahieren die 2. Gleichung von der 1. Gleichung und subtrahieren das Ergebnis von der 3. Gleichung. Wir erhalten


Somit ist 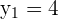 und
und 
4 Die Eckpunkte lauten also: 
Beweise, dass die Punkte  und
und  zu einem Kreis mit dem Mittelpunkt
zu einem Kreis mit dem Mittelpunkt  gehören.
gehören.
1 Die Punkte eines Kreises sind gleich weit vom Mittelpunkt entfernt. Überprüfe also, ob die Abstände zwischen den Punkten und dem Mittelpunkt gleich groß sind.
2 Wir berechnen die Abstände:

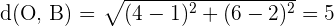
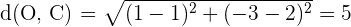
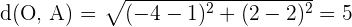
Damit ist sichergestellt, dass die vier Punkte zu einem Kreis mit dem Mittelpunkt  gehören
gehören
Klassifiziere das durch folgende Punkte bestimmte Dreieck: 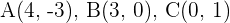 .
.
1 Wir zeichnen die Punkte ein
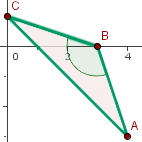
2 Wir berechnen die Abstände der Seiten


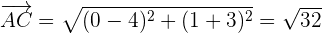
Dadurch wird sichergestellt, dass das Dreieck gleichschenklig ist.
3 Wir klassifizieren nach den Winkeln:
Wenn 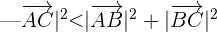 , ist es spitzwinklig.
, ist es spitzwinklig.
Wenn  , ist es rechtwinklig.
, ist es rechtwinklig.
Wenn 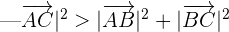 , ist es stumpfwinklig.
, ist es stumpfwinklig.
Da  , ist das Dreieck stumpfwinklig.
, ist das Dreieck stumpfwinklig.
Normiere folgende Vektoren:  .
.
1 Um einen Vektor zu normieren, müssen wir jede Koordinate des Vektors durch die Länge des Vektors teilen.
2 Wir berechnen die Längen der Vektoren
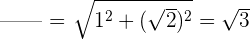
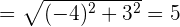

3 Wir normieren die Vektoren
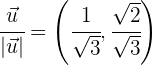 .
.
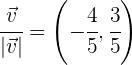 .
.
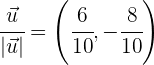 .
.
Bestimme  , wenn der Winkel, den
, wenn der Winkel, den  mit
mit 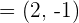 bildet: a)
bildet: a)  , b)
, b) 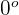 , c)
, c)  beträgt
beträgt
1 Für den Winkel von  muss
muss 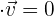 sein. Wir setzen die Werte der Vektoren ein und lösen nach
sein. Wir setzen die Werte der Vektoren ein und lösen nach  auf
auf

2 Für den Winkel von 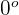 muss
muss  sein. Wir setzen die Werte der Koordinaten der Vektoren ein und lösen nach
sein. Wir setzen die Werte der Koordinaten der Vektoren ein und lösen nach  auf.
auf.
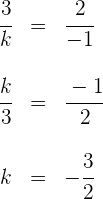
3 Für den Winkel von  muss
muss  sein. Wir setzen die Koordinatenwerte der Vektoren in die Gleichung für den von zwei Geraden gebildeten Winkel ein und lösen nach
sein. Wir setzen die Koordinatenwerte der Vektoren in die Gleichung für den von zwei Geraden gebildeten Winkel ein und lösen nach  auf
auf
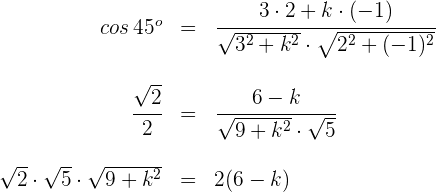
Wir quadrieren beide Seiten
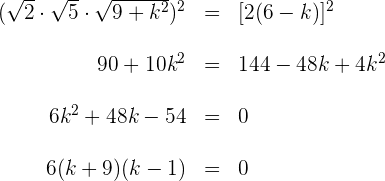
Die gesuchten Werte sind also 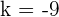 und
und 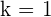
Wir berechnen die Abbildung des Vektors  auf den Vektor
auf den Vektor  , wobei
, wobei 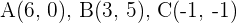 .
.
1 Wir stellen grafisch dar
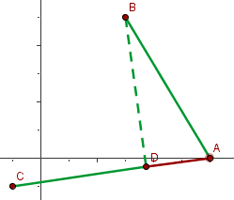
2 Um die Abbdildung zu berechnen, wenden wir  an. Wir setzen die Werte der Koordinaten der Vektoren ein und lösen
an. Wir setzen die Werte der Koordinaten der Vektoren ein und lösen
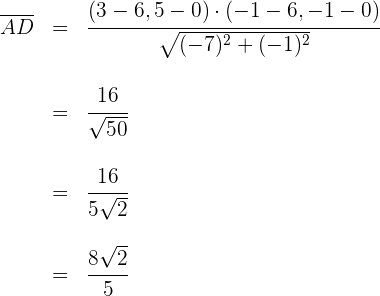
Überprüfe, ob das Segment, dass die Mittelpunkte der Seiten  und
und  des Dreiecks verbindet, folgende Eigenschaft erfüllt:
des Dreiecks verbindet, folgende Eigenschaft erfüllt: 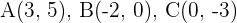 ist parallel zur Seite
ist parallel zur Seite  und gleich zu seiner Mitte.
und gleich zu seiner Mitte.
1 Wir stellen grafisch dar
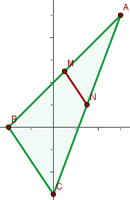
2 Wir berechnen den Vektor 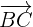
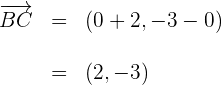
3 Wir berechnen die Mittelpunkte von  und
und 

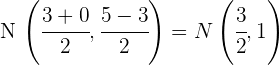
4 Wir berechnen den Vektor 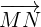
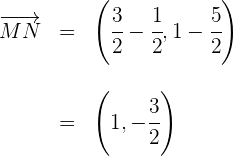
5 Zwei Vektoren sind parallel, wenn der Winkel, den sie bilden, 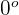 beträgt
beträgt
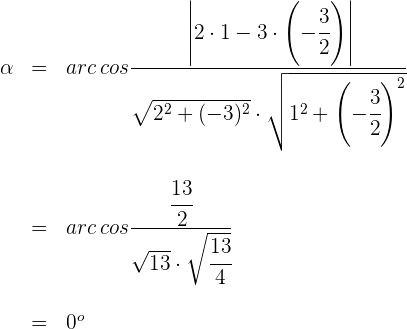
Somit sind die Vektoren parallel.
6 Wir berechnen die Längen der Vektoren 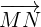 und
und 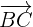
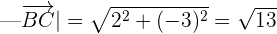
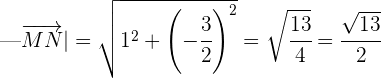
Somit ist die Länge von 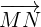 die Hälfte von
die Hälfte von 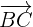
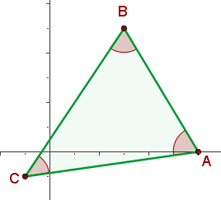
Berechne die Winkel des Dreiecks mit den Eckpunkten:  .
.
1 Wir stellen grafisch dar
2 Wir berechnen die Vektoren 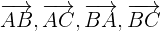
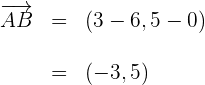
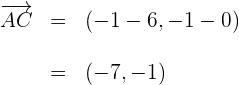
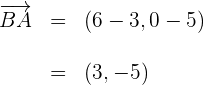
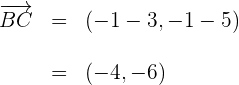
3 Wir berechnen den Winkel  , den die Vektoren
, den die Vektoren 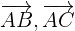 bilden
bilden
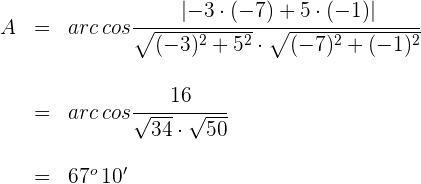
4 Wir berechnen den Winkel  , den die Winkel
, den die Winkel  bilden
bilden
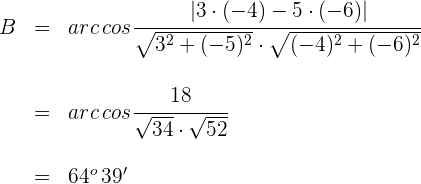
5 Wir berechnen den Winkel 
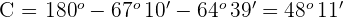
Gegeben sind die Vektoren 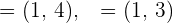 , die eine Basis bilden. Drücke auf dieser Basis den Vektor
, die eine Basis bilden. Drücke auf dieser Basis den Vektor 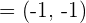 aus.
aus.
1 Wir schreiben 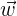 als Linearkombination von
als Linearkombination von  und
und 
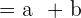
2 Wir setzen die Vektoren ein und berechnen

3 Wir erhalten ein Gleichungssystem
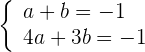
Wir multiplizieren die 1. Gleichung mit 4 und subtrahieren davon die 2. Gleichung. Wir erhalten
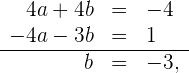
Wir setzen den erhaltenen Wert in eine der beiden Gleichungen ein und erhalten 
4 Die gesuchte Linearkombination ist
Berechne den Wert für  , sodass die Vektoren
, sodass die Vektoren  und
und  einen Winkel von
einen Winkel von  bilden.
bilden.
1 Für den Winkel von  muss
muss  sein. Wir setzen die Werte der Koordinaten der Vektoren in die Gleichung für den Winkel zwischen zwei Geraden ein und lösen nach
sein. Wir setzen die Werte der Koordinaten der Vektoren in die Gleichung für den Winkel zwischen zwei Geraden ein und lösen nach  auf.
auf.

2 Wir quadrieren beide Seiten
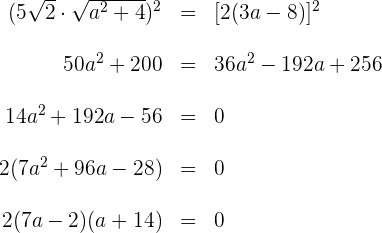
Somit sind die gesuchten Werte 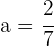 und
und 
Mit KI zusammenfassen:


