Ein Vektor  hat die Komponenten
hat die Komponenten 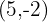 . Bestimme die Koordinaten von
. Bestimme die Koordinaten von  , wenn sein Endpunkt
, wenn sein Endpunkt  ist.
ist.
1
Da wir die Koordinaten von  nicht kennen, notieren wir sie in dieser Form:
nicht kennen, notieren wir sie in dieser Form:
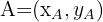 .
.
2
Wie wir wissen, berechnet man die Koordinaten eines Vektors, indem man den Startpunkt vom Endpunkt abzieht.
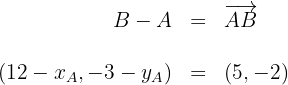
3
Wir erhalten zwei Gleichungen
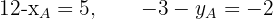
4
Wir lösen die beiden Gleichungen auf und erhalten folgende Koordinaten von  :
:
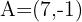
Gegeben sei der Vektor 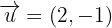 und zwei gleichwertige Vektoren
und zwei gleichwertige Vektoren  und
und 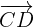 . Bestimme
. Bestimme  und
und  . Dabei ist
. Dabei ist 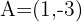 und
und  .
.
1
Da  gleichwertig sind, ist
gleichwertig sind, ist 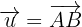 .
.
2
Da wir die Koordinaten von  nicht kennen, notieren wir sie als:
nicht kennen, notieren wir sie als:
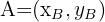 .
.
3
Die Koordinaten eines Vektors berechnet man, indem man den Startpunkt vom Endpunkt abzieht.
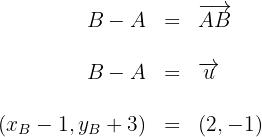
4
Wir erhalten zwei Gleichungen

5
Wir lösen die beiden Gleichungen auf und erhalten folgende Koordinaten von 

6
Wir lösen die Gleichung für  nach demselben Schema auf und erhalten
nach demselben Schema auf und erhalten  .
.
Bestimme den Abstand zwischen den Punkten 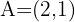 und
und 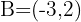 .
.
1
Die Formel zur Berechnung des Abstands zwischen zwei Punkten ist

2
Setze die Werte von  und
und  in die Abstandsformel ein und du erhältst
in die Abstandsformel ein und du erhältst
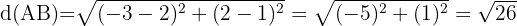
 ist ein Vektor mit den Komponenten
ist ein Vektor mit den Komponenten 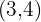 . Bestimme einen Einheitsvektor mit derselben Richtung und Orientierung.
. Bestimme einen Einheitsvektor mit derselben Richtung und Orientierung.
1
Die Formel für den Einheitsvektor ist
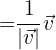
2
Berechne den Betrag von 

3
Setze den Wert in die Formel zur Berechnung des Einheitsvektors ein

Bestimme einen Einheitsvektor, der dieselbe Richtung wie der Vektor 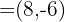 besitzt.
besitzt.
1
Die Formel für den Einheitsvektor ist
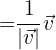
2
Berechne den Betrag von 

3
Setze den Wert in die Formel zur Berechnung des Einheitsvektors ein

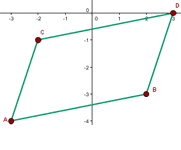
Berechne die Koordinaten von 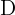 so, dass das Viereck mit den Eckpunkten
so, dass das Viereck mit den Eckpunkten  und
und 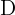 ein Parallelogramm ist.
ein Parallelogramm ist.
1
Die gegenüberliegenden Seiten eines Parallelogramms haben dieselbe Länge und Richtung, daher erhalten wir
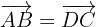
2
Da wir die Koordinaten von 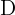 nicht kennen, notieren wir sie als
nicht kennen, notieren wir sie als
 .
.
3
Setze die Werte der Scheitelpunkte des Parallelogramms in die Vektorgleichung ein
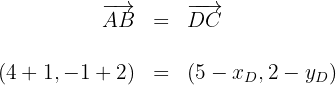
4
Wir erhalten zwei Gleichungen

5
Wir lösen die Gleichungen auf und erhalten folgende Koordinaten

Finde den Mittelpunkt der Strecke  mit den Endpunkten
mit den Endpunkten  und
und  .
.
1
Die Formeln zur Berechnung der Koordinaten des Mittelpunkts sind

2
Setze die Werte von  und
und  in die beiden Formeln ein
in die beiden Formeln ein
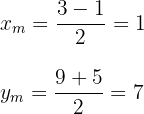
3
Der Mittelpunkt ist 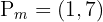 .
.
Bestimme die Koordinaten des Punktes  , wenn
, wenn 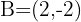 der Mittelpunkt von
der Mittelpunkt von  ist, und
ist, und 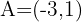 .
.
1
Die Formeln zur Berechnung der Koordinaten des Mittelpunkts sind

2
Setze die Werte von  und
und  in die beiden Formeln ein und berechne die erste Koordinate von
in die beiden Formeln ein und berechne die erste Koordinate von 
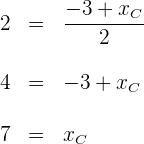
3
Die zweite Koordinate von  ist
ist
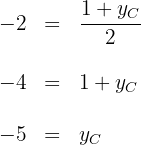
4
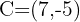 ist
ist
Finde heraus, ob die Punkte  und
und  kollinear sind.
kollinear sind.
1
Die Punkte 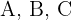 sind kollinear, wenn die Steigungen der Geraden
sind kollinear, wenn die Steigungen der Geraden  und
und  gleich sind.
gleich sind.

2
Da beide Steigungen gleich sind, sind die drei Punkte kollinear.
Berechne den Wert von  , für den die Punkte
, für den die Punkte 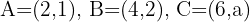 kolinear sind.
kolinear sind.
1
Die Punkte 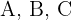 sind kolinear, wenn die Steigungen der Geraden
sind kolinear, wenn die Steigungen der Geraden  und
und  gleich sind.
gleich sind.
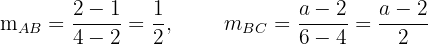
2
Da beide Steigungswerte gleich sind, setzen wir die Terme miteinander gleich und lösen nach  auf
auf
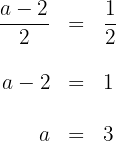
Gegeben seien die Punkte 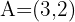 und
und 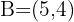 . Bestimme einen Punkt
. Bestimme einen Punkt  , der kollinear zu
, der kollinear zu  und
und ist und mit dem man
ist und mit dem man  erhält.
erhält.
1
Aus den vorherigen Konditionen erhalten wir folgende Gleichung
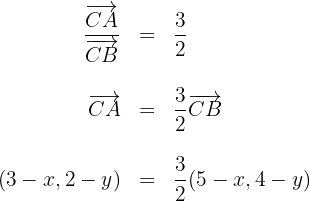
2
Setze beide Ausdrücke Koordinate für Koordinate gleich und du erhältst
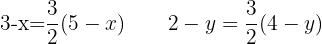
3
Löse die beiden Gleichungen, um die Koordinaten von  zu erhalten
zu erhalten
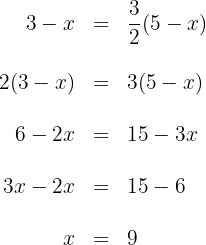
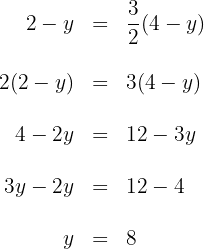
Gegeben sei ein Dreieck mit den Eckpunkten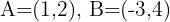 und
und  . Bestimme die Koordinaten seines Schwerpunkts.
. Bestimme die Koordinaten seines Schwerpunkts.
1
Die Formel, um den Schwerpunkt zu berechnen, ist

2
Setze die Werte der Eckpunkte in die Formel ein und du erhältst

Gegeben sei ein Dreieck mit zwei Eckpunkten 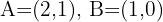 und dem Schwerpunkt
und dem Schwerpunkt 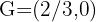 . Berechne den dritten Eckpunkt.
. Berechne den dritten Eckpunkt.
1
Die Formel, um den Schwerpunkt zu berechnen, ist

2
Setze die Werte des Schwerpunkts und der Eckpunkte in die Formel ein und du erhältst zwei Gleichungen

3
Löse beide Gleichungen auf und du erhältst den dritten Eckpunkt 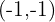 .
.
Finde den Spiegelpunkt des Punktes 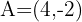 an
an 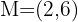 .
.
1
Den Spiegelpunkt von  notieren wir als
notieren wir als 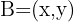 . Es gilt außerdem:
. Es gilt außerdem: 
2
Durch Einsetzen der Werte der Punkte erhalten wir zwei Gleichungen, die den Koordinaten der Vektoren entsprechen

3
Löse beide Gleichungen auf und du erhältst  .
.
Finde den Spiegelpunkt des Punktes  an
an 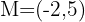 .
.
1
Den Spiegelpunkt von  notieren wir als
notieren wir als 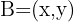 . Es gilt außerdem:
. Es gilt außerdem: 
2
Durch Einsetzen der Werte der Punkte erhalten wir zwei Gleichungen, die den Koordinaten der Vektoren entsprechen

3
Löse beide Gleichungen auf und du erhältst 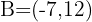 .
.
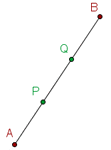
Welche Punkte  und
und  teilen eine Strecke mit den Endpunkten
teilen eine Strecke mit den Endpunkten 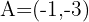 und
und 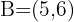 in drei gleich lange Segmente?
in drei gleich lange Segmente?
1
In Vektorschreibweise erhalten wir

2
Durch Einsetzen der Werte der Punkte erhalten wir zwei Gleichungen, die den Koordinaten der Vektoren entsprechen

3
Löse beide Gleichungen auf und du erhältst 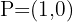 .
.
4
Um die Koordinaten von  zu finden, notieren wir
zu finden, notieren wir
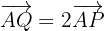
5
Durch Einsetzen der Werte der Punkte erhalten wir zwei Gleichungen, die den Koordinaten der Vektoren entsprechen

6
Löse beide Gleichungen auf und du erhältst  .
.
Die Strecke  mit den Endpunkten
mit den Endpunkten 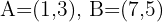 wird in vier gleich lange Segmente geteilt. Welche sind die Koordinaten der Punkte, die sie teilen?
wird in vier gleich lange Segmente geteilt. Welche sind die Koordinaten der Punkte, die sie teilen?
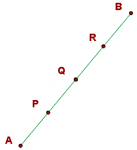
1
Man kann erkennen, dass  der Mittelpunkt der Strecke
der Mittelpunkt der Strecke  ist
ist
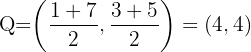
2
 ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke 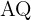

3
 ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke 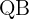
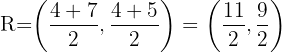
Mit KI zusammenfassen:



