Bestimme den Spiegelpunkt von 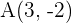 in Bezug auf
in Bezug auf 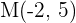 .
.
1 Wir berechnen den Spiegelpunkt  . Hierfür gilt
. Hierfür gilt 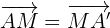

2 Wir setzen die Koordinaten gleich und bestimmen die Variablen 
Für die erste Koordinate gilt

Für die zweite Koordinate gilt
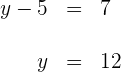
3 Der Spiegelpunkt hat die Koordinaten
hat die Koordinaten
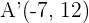
Gegeben sind die Eckpunkte  eines Dreiecks und der Schwerpunkt
eines Dreiecks und der Schwerpunkt  . Berechne den dritten Eckpunkt.
. Berechne den dritten Eckpunkt.
1 Die Formel für den Schwerpunkt eines Dreiecks mit den Eckpunkten 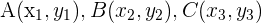 lautet
lautet

2 Wir berechnen den Schwerpunkt mithilfe des dritten Eckpunktes 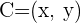 . Hierzu setzen wir in die vorhergehende Formel ein
. Hierzu setzen wir in die vorhergehende Formel ein
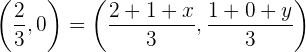
3 Wir setzen die Koordinaten gleich und lösen nach den Variablen  auf
auf
Für die erste Koordinate gilt
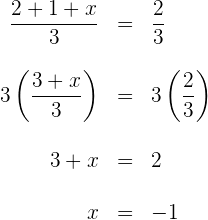
Für die zweite Koordinate gilt
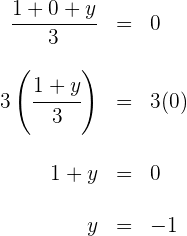
4 Der dritte Eckpunkt lautet
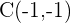
Gegeben sind die Punkte  und
und 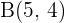 . Bestimme einen Punkt
. Bestimme einen Punkt  anhand der Punkte
anhand der Punkte  und
und  , sodass wir
, sodass wir 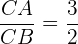 erhalten
erhalten
1 Da 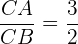 , setzen wir die Werte für
, setzen wir die Werte für  und
und 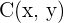 ein und erhalten
ein und erhalten
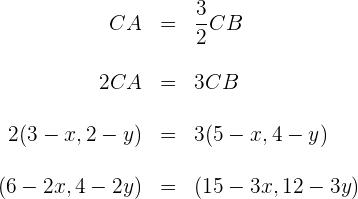
2 Wir setzen die Koordinaten gleich und lösen nach den Variablen  auf
auf
Für die erste Koordinate gilt
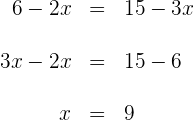
Für die zweite Koordinate gilt
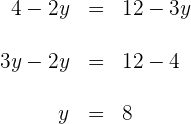
3 Der gesuchte Punkt ist 
Berechne die Koordinaten von 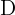 für das Viereck mit den Eckpunkten:
für das Viereck mit den Eckpunkten:  und
und 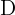 bilden ein Parallelogramm.
bilden ein Parallelogramm.
1 Um die Koordinaten von  zu bestimmen, nutzen wir die Tatsache, dass es sich um die gegenüberliegenden Seiten eines Parallelogramms handelt. Seine Vektoren sind daher
zu bestimmen, nutzen wir die Tatsache, dass es sich um die gegenüberliegenden Seiten eines Parallelogramms handelt. Seine Vektoren sind daher
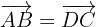
2 Wir setzen ein und erhalten
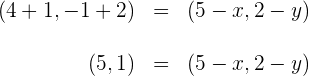
3 Wir setzen die Koordinaten gleich und lösen nach den Variablen  auf
auf
Für die erste Koordinate gilt
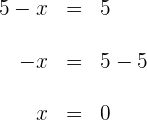
Für die zweite Koordinate gilt
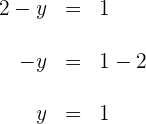
4 Der gesuchte Punkt ist 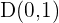
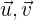 bilden eine Orthonormalbasis. Berechne:
bilden eine Orthonormalbasis. Berechne:
a 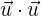
b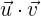
c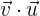
d 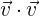
1 Da 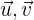 zueienander orthonormal sind, stehen sie senkrecht aufeinander. Sie bilden deshalb einen Winkel von
zueienander orthonormal sind, stehen sie senkrecht aufeinander. Sie bilden deshalb einen Winkel von  und ihre Länge ist 1. Somit gilt
und ihre Länge ist 1. Somit gilt 
2 Um die gewünschten Produkte zu bestimmen, wenden wir die Formel an
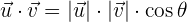
 entspricht dem Winkel zwischen
entspricht dem Winkel zwischen  und
und 
3 Wir setzen in die Formel ein und verwenden den entsprechenden Wert  , wenn die Vektoren gleich sind und
, wenn die Vektoren gleich sind und  , wenn sie unterschiedlich sind
, wenn sie unterschiedlich sind
a 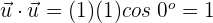
b 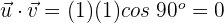
c 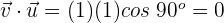
d 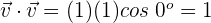
Gegeben sind die Vektoren  . Berechne
. Berechne  so, dass die Vektoren
so, dass die Vektoren  folgende Eigenschaften besitzen:
folgende Eigenschaften besitzen:
a Sie stehen senkrecht zueinander.
b Sie sind parallel.
c Sie bilden einen 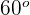 -Winkel.
-Winkel.
a Senkrecht: Zwei Vektoren stehen zueinander senkrecht, wenn ihr Produkt null ist
Wir multiplizieren aus und bestimmen die Variable 
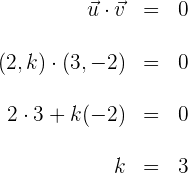
b Parallel: Zwei Vektoren sind parallel, wenn ihre Elemente proportional sind. Das heißt,
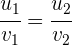
Wir setzen gleich und bestimmen die Variable 
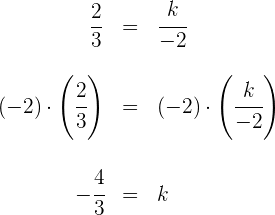
c Sie bilden einen 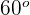 -Winkel: Wir setzen die Werte in die Formel ein
-Winkel: Wir setzen die Werte in die Formel ein
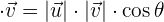
mit 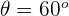
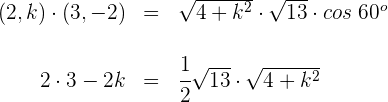
Wir quadrieren beide Seiten und vereinfachen
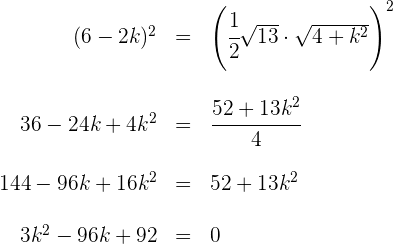
Wir lösen mithilfe der Formel zur Bestimmung der Nullstellen der quadratischen Gleichung
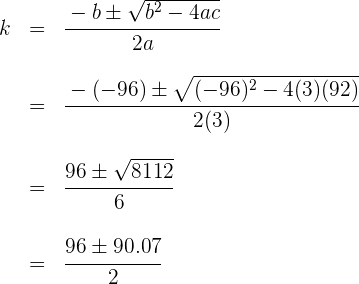
Die Nullstellen der quadratischen Gleichung sind  . Allerdings erfüllt nur
. Allerdings erfüllt nur 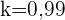 die Gleichung und ist somit der gesuchte Wert für
die Gleichung und ist somit der gesuchte Wert für  .
.
Berechne den Wert für  .
. 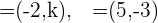 und
und 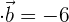 sind dabei bekannt.
sind dabei bekannt.
1Wir berechnen das Produkt der Vektoren
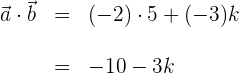
2Wir setzen das Ergebnis gleich 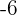 und lösen nach
und lösen nach  auf
auf
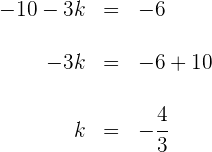
Gegeben ist die Orthonormalbasis 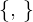 der Ebene. Berechne den Wert für
der Ebene. Berechne den Wert für  so, dass die Vektoren
so, dass die Vektoren 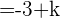 und
und 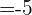 zueinander orthogonal sind.
zueinander orthogonal sind.
1Da die Basis orthonormal ist, gilt
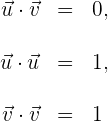
2Wir berechnen das Skalarprodukt aus  und
und 
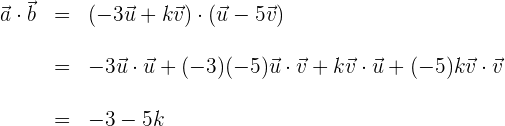
3 Zwei Vektoren sind zueinander orthogonal, wenn ihr Produkt null ist. Wir setzen ein und bestimmen 
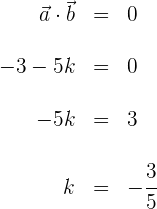
Berechne die Projektion des Vektors  auf den Vektor
auf den Vektor 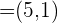 .
.
1Die Formel der Projektion des Vektors  auf den Vektor
auf den Vektor  ist gegeben durch
ist gegeben durch
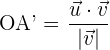
2Wir berechnen das Produkt der Vektoren
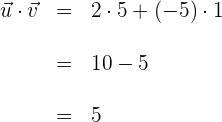
3Wir berechnen die Länge des Vektors
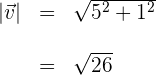
4Wir setzen die Werte in die Formel der Projektion ein
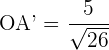
Bestimme einen Einheitsvektor  , der in dieselbe Richtung zeigt wie der Vektor
, der in dieselbe Richtung zeigt wie der Vektor 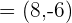 .
.
1Die Formel eines Einheitsvektors ist gegeben durch
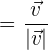
2Wir berechnen die Länge des Vektors 
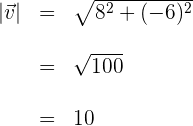
3Wir setzen in die Formel des Einheitsvektors ein
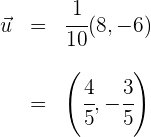
Mit KI zusammenfassen:



