Kapitel
- Arten von Vektoren
- Koordinaten eines Vektors
- Betrag eines Vektors
- Linearkombinationen von Vektoren
- Bezugssystem
- Basis
- Koordinaten des Mittelpunkts eines Segments
- Voraussetzung, damit sich drei Punkte auf einer Geraden befinden
- Punktsymmetrie
- Koordinaten des Schwerpunkts
- Unterteilung eines Segments in einem bestimmten Verhältnis
- Skalarprodukt
- Ein Vektor
ist ein mit einer Richtung versehenes Segment, das vom Punkt A (Ursprung) zum Punkt B (Spitze) geht. - Ein festgelegter Vektor ist null, wenn der Ursprung und sein Endpunkt zusammenfallen.
- Der Betrag des Vektors ist die Länge des Segments
. - Der Betrag wird mit dargestellt.
- Die Richtung des Vektors ist die Richtung der Geraden, die den Vektor enthält, oder einer zu ihm parallelen Geraden.
- Die Orientierung des Vektors verläuft vom Ursprung
zum Endpunkt 
.
Arten von Vektoren
1 Äquivalente Vektoren:
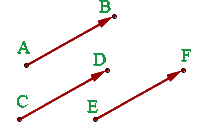
Zwei Vektoren sind äquivalent, wenn sie denselben Betrag, dieselbe Richtung und dieselbe Orientierung haben.
2Freie Vektoren:
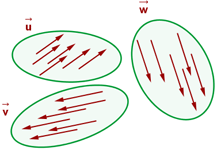
Die Menge aller äquivalenten Vektoren wird als freier Vektor bezeichnet. Jeder feste Vektor ist ein Vertreter des freien Vektors.
Koordinaten eines Vektors
1Ortsvektor eines Punktes in der Koordinatenebene
Der Vektor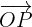 
, der den Ursprung 
mit einem Punkt 
verbindet, heißt Ortsvektor des Punkts .
2Koordinaten oder Komponenten eines Vektors in der Ebene
Wenn die Koordianten von und wie folgt lauten:
Die Koordinaten oder Komponenten des Vektors sind die Koordinaten des Endpunkts minus die Koordinaten des Ursprungs.
Betrag eines Vektors
Der Betrag eines Vektors ist die Länge des orientierten Segments, das ihn definiert.
Der Betrag eines Vektors ist immer eine positive Zahl und nur der Nullvektor hat einen Betrag von 0.
Berechnung des Betrags, wenn seine Komponenten bekannt sind
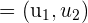
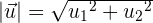
Berechnung des Betrags, wenn die Koordinaten der Punkte bekannt sind
Distanz zwischen Punkten
Die Distanz zwischen zwei Punkten ist gleich dem Betrag des Vektors, der diese Punkte als Endpunkte hat.
Einheit als Betrag
Einheitsvektoren haben als Betrag die Einheit.
Summe von Vektoren
Um zwei freie Vektoren 
und 
zu addieren, werden zwei Vektoren als Repräsentanten so gewählt, dass der Endpunkt des einen mit dem Anfangspunkt des anderen Vektors zusammenfällt.
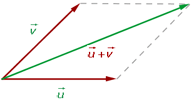
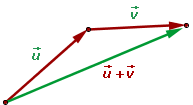
Parallelogrammgleichung
Man nimmt zwei Vektoren mit gemeinsamem Ursprung als Repräsentanten, zieht Geraden parallel zu den Vektoren und erhält ein Parallelogramm, dessen Diagonale mit der Summe der Vektoren übereinstimmt.
Um zwei Vektoren zu addieren, werden ihre jeweiligen Komponenten addiert.
Vektoren subtrahieren
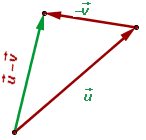
Um zwei freie Vektoren und zu subtrahieren, addieren wir mit dem Gegenteil von .
Die Komponenten des Subtraktionsvektors erhält man durch Subtraktion der Komponenten der Vektoren.
Produkt aus Zahl und Vektor
Das Produkt aus einer Zahl 
und einem Vektor ergibt einen weiteren Vektor:
1 Mit derselben Richtung wie der Vektor .
2 Mit derselben Orientierung wie der Vektor , wenn positiv ist.
3 Mit entgegengesetzter Orientierung des Vektors , wenn negativ ist.
5 Mit dem Betrag 
Die Komponenten des resultierenden Vektors erhält man, indem man die Komponenten des Vektors mit multipliziert.
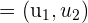
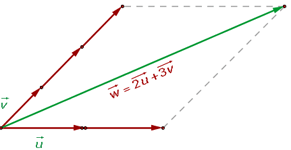
Linearkombinationen von Vektoren
Gegeben sind die Vektoren: und sowie zwei Zahlen: 
und 
. Der Vektor 
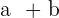ist eine Linearkombination aus und .
Jeder Vektor kann als Linearkombination von zwei anderen Vektoren mit unterschiedlichen Richtungen dargestellt werden.
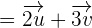
Diese Linearkombination ist einzigartig.
Bezugssystem
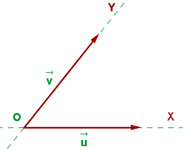
In der Ebene besteht ein Bezugssystem aus einem Punkt der Ebene und einer Basis ( , ).
Der Punkt des Bezugssystems heißt Ursprung.
Die Vektoren , sind nicht parallel und bilden die Basis.
Basis
1Orthogonal
Die Basisvektoren stehen senkrecht zueinander, haben aber unterschiedliche Beträge.
2 Orthonormal
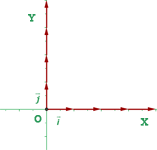
Die Vektoren der Basis stehen senkrecht zueinander und sind einheitlich, das heißt, sie haben den Betrag 
.
Sie werden mit den Buchstaben 
dargestellt.
.
.
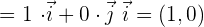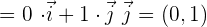Die Geraden 
, 
werden Koordinatenachsen genannt.
Koordinaten des Mittelpunkts eines Segments
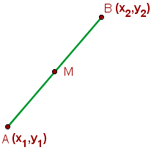
Die Koordinaten des Mittelpunkts eines Segments sind die Halbsumme der Koordinaten der Endpunkte des Segments.
Voraussetzung, damit sich drei Punkte auf einer Geraden befinden
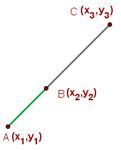
Die Punkte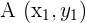 
, 
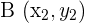und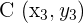 
befinden sich immer auf einer Geraden, wenn die Vektoren und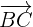 
dieselbe Richtung haben. Dies tritt auf, wenn ihre Koordinaten proportional sind.
Punktsymmetrie
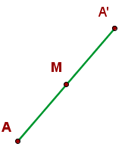
Wenn 
symmetrisch zu in Bezug auf 
ist, ist der Mittelpunkt des Segments 
. Somit gilt folgende Gleichheit:
Koordinaten des Schwerpunkts
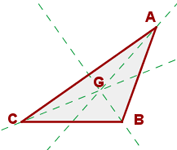
Das Baryzentrum oder der Schwerpunkt eines Dreiecks ist der Schnittpunkt seiner Mittellinien.
Die Koordinaten des Schwerpunkts sind:
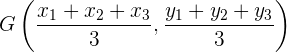
Unterteilung eines Segments in einem bestimmten Verhältnis
Ein Segment in einem gegebenen Verhältnis 
zu unterteilen, bedeutet, einen Punkt der Geraden zu bestimmen, der das Segment enthält, sodass die zwei Teile 
und 
sich im Verhältnis zueinander befinden:
Skalarprodukt
Das Skalarprodukt zweier Vektoren ist eine reelle Zahl, die sich aus der Multiplikation des Produkts ihrer Beträge mit dem Kosinus des Winkels, den sie bilden, ergibt.
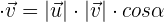
1Analytischer Ausdruck des Skalarproduktes
2Analytischer Ausdruck für den Betrag eines Vektors
3 Analytischer Ausdruck für den Winkel zwischen zwei Vektoren
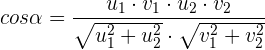
4 Analytische Bedingung für die Orthogonalität von zwei Vektoren
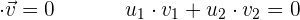
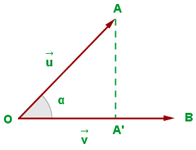
Projektion
Das Produkt zweier Vektoren, die nicht null sind, ist gleich dem Betrag des einen Vektors mal der Projektion des anderen Vektors auf ihn.
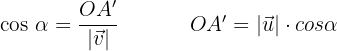
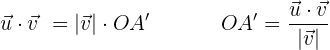
Eigenschaften des Skalarprodukts
1 Kommutativ
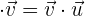
2 Assoziativ
3 Distributiv
4 Das Skalarprodukt eines Vektors, der nicht null ist, ist für sich immer positiv.
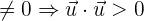
Wenn Du individuelle Hilfe zum Thema Vektoren brauchst, kannst Du Deine:n ideale:n Lehrer:in für einen Mathekurs finden, der auf Deine Bedürfnisse zugeschnitten ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
