Kapitel
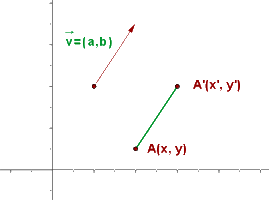
in der Ebene einem anderen Punkt 
, ebenfalls in der Ebene, entspricht, so dass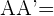 
. 
ist dabei der Vektor, der die Verschiebung definiert.
Die Verschiebung wird mit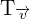 
angegeben und somit 
.
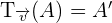Der Punkt ist die Verschiebung des Punktes .
Ein Punkt und seine Verschiebung sind homolog.
Koordinaten eines Punktes durch Verschiebung
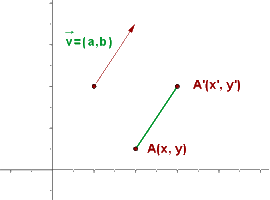
Die Verschiebung 
, die durch den Vektor vom Punkt zum Punkt definiert ist, lässt sich durch die folgende Formel verstehen.
Zunächst beschreiben wir, wie man die Daten richtig notiert:
.
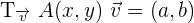Der Punkt ist gleich dem Punkt plus den Vektor :
.
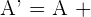Somit
,
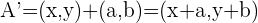wobei
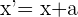
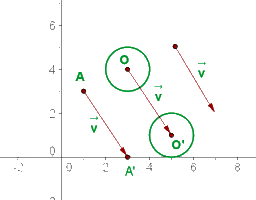
Beispiel für die Verschiebung eines Vektors
In der grafischen Darstellung ist der Punkt A zu sehen, der durch den Vektor auf den Punkt A' übertragen wird.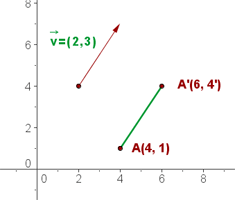
Die Daten der Verschiebung lauten wie folgt:
.
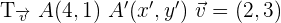Wir wissen, dass die Koordinate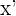 
nach der Formel 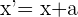berechnet wird.
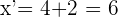
Wir berechnen nun 
mit der Formel
Die Koordinaten des Punkts sind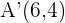 
Verschiebung einer Geraden
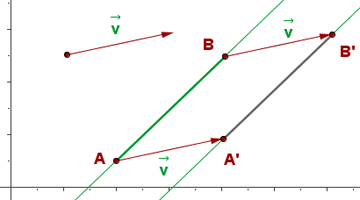
Eine Gerade, mit mit einer Verschiebung verschoben wird, ist eine parallele Gerade.
Verschiebung eines Kreises
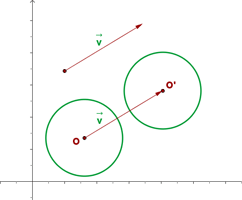
Die Homologie eines Kreises durch eine Verschiebung ist ein anderer Kreis mit gleichem Radius, der als Mittelpunkt den Punkt hat, der homolog zum Mittelpunkt des ursprünglichen Kreises ist.
Zusammensetzung von Verschiebungen
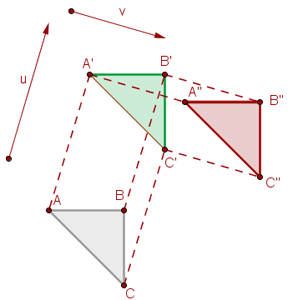
Wenn man nacheinander zwei Verschiebungen der Vektoren und 
vornimmt, erhält man eine weitere Verschiebung, deren Vektor die Summe der Vektoren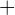 
ist, wobei:
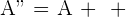
Aufgaben zu Verschiebungen
Eine Verschiebung in der Ebene ist durch einen Vektor 
gegeben
- Ermittle die Abbildung dieser Verschiebung von einem Punkt
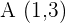. - Ermittle die Verschiebung eines Kreises mit Mittelpunkt
und Radius 
.
a Ermittle die Abbildung dieser Verschiebung von einem Punkt 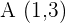. Wir schreiben zunächst die Daten des Problems: 
.
Wir verwenden die Formel 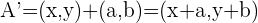zur Berechnung der Abbildung und erhalten:
.
.
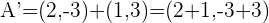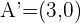b Ermittle die Verschiebung eines Kreises mit Mittelpunkt und Radius .
Wir schreiben zunächst die Daten des Problems:
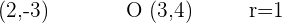
entspricht den Koordinaten des Mittelpunktes des Kreises und r ist sein Radius.
Mit der gleichen Formel wie für Punkt A berechnen wir die Abbildung von O
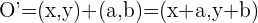und erhalten:
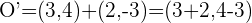
und die Abbildung des Radius 
ist weiterhin gleich 
Bei einer Verschiebung druch den Vektor wird ein Punkt 
zu einem Punkt 
.
Berechne:
- Die Verschiebung des Punktes
. - Die Verschiebung eines Kreises mit Mittelpunkt
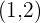und Radius 
.
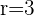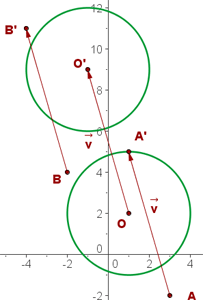
a Die Verschiebung des Punktes . Wir schreiben zunächst die Daten des Problems:
Damit wir die Verschiebung des Punktes 
schreiben können, die wir mit 
benennen, müssen wir herausfinden, welcher der Vektor ist.
Wir wissen, dass der Vektor die Koordinaten 
hat.
Mithilfe der Verschiebungsformel vervollständigen wird die bekannten Daten (die Koordinaten der Punkte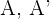 
:
.
.
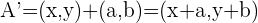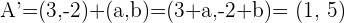Wir wissen also, dass:
.
.
.
.
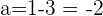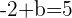Mit den Koordinaten des Vektors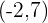 
kann man die Verschiebung des Punktes 
berechnen.
Wir verwenden die gleiche Formel
.
Wir schreiben die uns bekannten Daten:
,
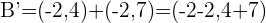und erhalten:
.
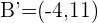b Die Verschiebung eines Kreises mit Mittelpunkt 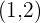und Radius .
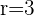Zunächst schreiben wir die Daten des Problems:
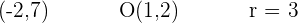
Und wir berechnen die Verschiebung des Kreises, die wir mit 
notieren, mit der gleichen Formel:
.
.
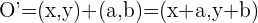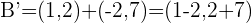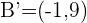und 
gleich .
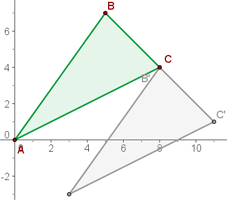
Eine Verschiebung hat den Vektor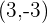 
. Finde die Verschiebung der Figur eines Dreiecks, dessen Eckpunkte wie folgt sind:
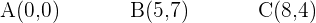
Um die Verschiebung der Figur zu zeichnen, müssen wir die Koordinaten der Punkte herausfinden. Eine Verschiebung hat den Vektor 
und 
. Zunächst schreiben wir die Daten des Problems: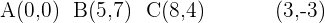 
Mit der Formel berechnen wir jede der Koordinaten: .
.
.
.
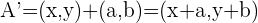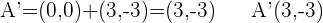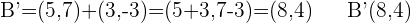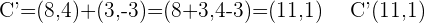Mit den Koordinaten können wir nun die Figur zeichnen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
