
Definition linear unabhängiger Vektoren
Mehrere freie Vektoren  sind linear unabhängig, wenn keiner von ihnen als Linearkombination der verbleibenen Vektoren geschrieben werden kann.
sind linear unabhängig, wenn keiner von ihnen als Linearkombination der verbleibenen Vektoren geschrieben werden kann.
Das bedeutet, dass, wenn die Linearkombination der  Vektoren gleich dem Nullvektor ist, dann jeder der Koeffizienten der Linearkombination null ist
Vektoren gleich dem Nullvektor ist, dann jeder der Koeffizienten der Linearkombination null ist

Linear unabhängige Vektoren haben unterschiedliche Richtungen und ihre Komponenten sind nicht proportional.
Eine weitere Möglichkeit, um festzustellen, ob Vektoren linear unabhängig sind, besteht darin, die Determinante der Matrix ihrer Komponenten zu berechnen. Ist diese ungleich null, sind die Vektoren linear unabhängig; andernfalls gelten die Vektoren als linear abhängig.

Aufgaben zu linear unabhängigen Vektoren
Untersuche, ob die Vektoren linear abhängig oder unabhängig sind:
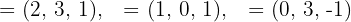 .
.
1Wir schreiben die Komponentenmatrix
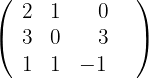
2Wir berechnen die Determinante der Komponentenmatrix
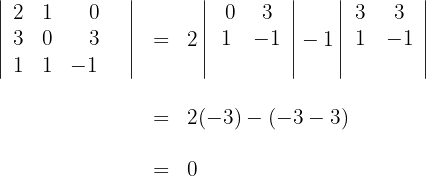
3Da die Determinante null ist, schließen wir daraus, dass die Vektoren linear abhängig sind.
Gegeben sind  . Zeige, dass diese Vektoren linear unabhängig sind, und drücke den Vektor
. Zeige, dass diese Vektoren linear unabhängig sind, und drücke den Vektor 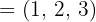 als Linearkombination dieser Vektoren aus.
als Linearkombination dieser Vektoren aus.
1Wir schreiben die Komponentenmatrix
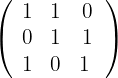
2Wir berechnen die Determinante der Komponentenmatrix

3Da die Determinante ungleich null ist, schließen wir daraus, dass die Vektoren linear unabhängig sind.
4Um 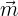 als Linearkombination von
als Linearkombination von  auszudrücken, schreiben wir diesen Ausdruck
auszudrücken, schreiben wir diesen Ausdruck

5Wir führen die Rechenoperationen auf der rechten Seite der Gleichung durch
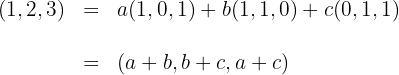
6Wir setzen die Koordinaten gleich und erhalten folgendes Gleichungssystem

7Wir addieren Glied für Glied der drei Gleichungen und vereinfachen. Wir erhalten

8Von der erhaltenen Gleichung subtrahieren wir jede der Gleichungen und erhalten

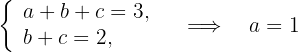
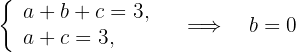
Somit ist 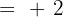
Mit KI zusammenfassen:












