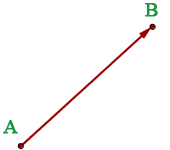
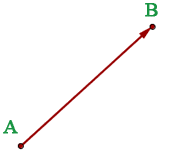
Ein Vektor 
ist ein mit einer Richtung versehenes Segment, das vom Punkt 
(Ursprungspunkt) zum Punkt 
(Endpunkt) verläuft.
Bestandteile eines Vektors
1 Richtung eines Vektors: Die Richtung eines Vektors ist gleich der Richtung der Geraden, auf der er verläuft, sowie aller dazu parallelen Geraden.
2 Orientierung eines Vektors: Die Orientierung eines Vektors ist durch den Verlauf des Vektors von seinem Anfangspunkt zu seinem Endpunkt gegeben.
3 Modul eines Vektors:
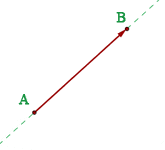
Das Modul des Vektors ist durch die Länge des Segments 
gegeben und wir als 
dargestellt.
Das Modul eines Vektors ist immer größer oder gleich Null.
Berechnung des Moduls eines Vektors auf Basis seiner Komponenten
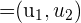
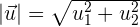
Beispiel
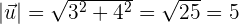
Berechnung des Moduls eines Vektors auf Basis der Koordinaten der daraufliegenden Punkte
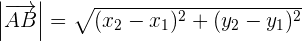
Beispiel
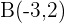
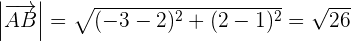
4 Koordinaten eines Vektors
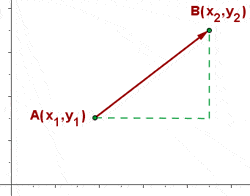
Wenn die Koordinaten der Endpunkte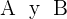 
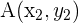sind,
berechnen sich die Koordinaten des Vektors aus den Koordinaten des Endpunktes minus den Koordinaten des Ursprungspunktes.
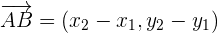
Beispiel:
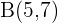
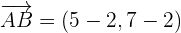
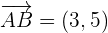
Arten von Vektoren
1 Äquipollente Vektoren
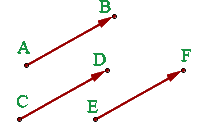
Zwei Vektoren sind äquipollent (gleichwertig), wenn sie dasselbe Modul und dieselbe Richtung und Orientierung aufweisen.
2 Freie Vektoren
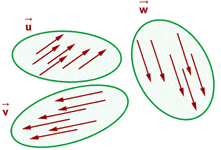
Die Menge aller äquipollenten Vektoren nennt man freien Vektor. Jeder der äquipollenten Vektoren ist Teil des freien Vektors.
3 Ortsgebundene Vektoren
Ein ortsgebundener Vektor stellt einen freien Vektor dar, dessen Eigenschaften an einen bestimmten Punkt gebunden sind. Ortsgebundene Vektoren besitzen dasselbe Modul, dieselbe Richtung und Orientierung sowie denselben Ursprung.
4 Linienflüchtige Vektoren
Linienflüchtige Vektoren sind freie Vektoren, die an ihre Wirkungslinie gebunden sind. Sie besitzen dasselbe Modul, dieselbe Richtung und Orientierung und liegen auf derselben Geraden.
5 Gegenvektoren
Gegenvektoren besitzen dasselbe Modul, dieselbe Richtung, aber eine andere Orientierung.
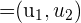
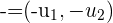
6 Einheitsvektoren
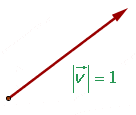
Die Länge eines Einheitsvektors ist immer gleich eins.
Um den Einheitsvektor eines Vektors mit derselben Richtung und Orientierung zu erhalten, teilt man diesen durch seine Länge.
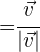
7 Richtungsvektoren
Richtungsvektoren haben denselben Ursprung.
8 Ortsvektoren
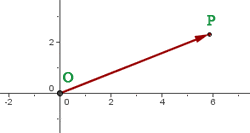
Der Vektor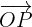 
, der vom Koordinatenursprung 
zum Punkt 
verläuft, nennt sich Ortsvektor des Punktes .
9 Linear abhängige Vektoren:
Freie Vektoren im Raum sind dann linear abhängig, wenn die Linearkombination aus ihnen gleich dem Nullvektor ist, ohne dass dabei alle Koeffizienten des Linearkombination gleich Null sind.
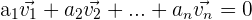
10 Linear abhängige Vektoren
Freie Vektoren im Raum sind dann linear unabhängig, wenn keine von ihnen als Linearkombination den anderen ausgedrückt werden kann.
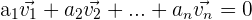
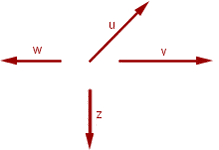
11 Orthogonale Vektoren
Zwei Vekotren sind orthogonal, wenn ihr Skalarprodukt gleich Null ist.
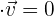
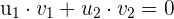
12 Orthonormale Vektoren
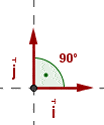
Zwei Vektoren sind orthonormal, wenn
a ihr Skalarprodukt gleich Null ist.
b beide Vektoren EInheitsvektoren sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
