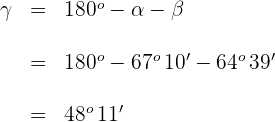Formel zur Berechnung des Winkels zwischen zwei Vektoren
Der Winkel, den zwei Vektoren  und
und  bilden, ist durch folgenden Ausdruck gegeben:
bilden, ist durch folgenden Ausdruck gegeben:
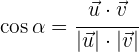
Der Ausdruck in Abhängigkeit der Koordinaten lautet

Beispiel: Bestimme den Winkel zwischen den Vektoren  und
und 
1Um die Formel zur Bestimmung des Winkels zwischen zwei Vektoren anzuwenden, berechnen wir zunächst das Produkt der beiden Vektoren
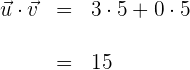
2Wir berechnen den Betrag des ersten Vektors
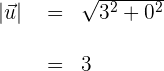
3Wir berechnen den Betrag des zweiten Vektors

4Wir setzen die erhaltenen Werte in die Formel für die Berechnung des Winkels  zwischen zwei Vektoren ein
zwischen zwei Vektoren ein
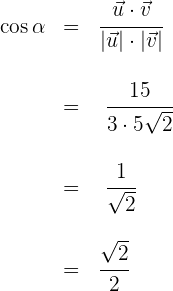
5Der Wert  , der die vorherige Gleichung erfüllt, ist
, der die vorherige Gleichung erfüllt, ist 
Aufgaben
Berechne das Skalarprodukt und den Winkel, den die Vektoren  bilden.
bilden.
1 Um die Formel zur Bestimmung des Winkels zwischen zwei Vektoren anzuwenden, berechnen wir zunächst das Produkt der beiden Vektoren

2 Wir berechnen den Betrag des ersten Vektors

3 Wir berechnen den Betrag des zweiten Vektors

4 Wir setzen die vorher ermittelten Werte in die Formel des Winkels  zwischen zwei Vektoren ein
zwischen zwei Vektoren ein

5 Der Wert , der die vorhergehende Gleichung erfüllt, ist
, der die vorhergehende Gleichung erfüllt, ist 
Berechne das Skalarprodukt und den Winkel, den die Vektoren  bilden.
bilden.
1 Um die Formel zur Bestimmung des Winkels zwischen zwei Vektoren anzuwenden, berechnen wir zunächst das Produkt der beiden Vektoren

2 Wir berechnen den Betrag des ersten Vektors
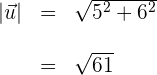
3 Wir berechnen den Betrag des zweiten Vektors

4 Wir setzen die vorher ermittelten Werte in die Formel des Winkels  zwischen zwei Vektoren ein
zwischen zwei Vektoren ein
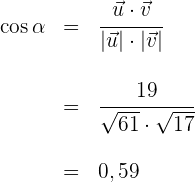
5 Der Wert  , der die vorhergehende Gleichung erfüllt, ist
, der die vorhergehende Gleichung erfüllt, ist 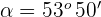
Berechne das Skalarprodukt und den Winkel, den die Vektoren  bilden.
bilden.
1 Um die Formel zur Bestimmung des Winkels zwischen zwei Vektoren anzuwenden, berechnen wir zunächst das Produkt der beiden Vektoren
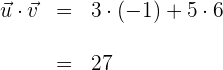
2 Wir berechnen den Betrag des ersten Vektors

3 Wir berechnen den Betrag des zweiten Vektors
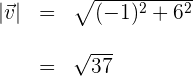
4 Wir setzen die vorher ermittelten Werte in die Formel des Winkels  zwischen zwei Vektoren ein
zwischen zwei Vektoren ein
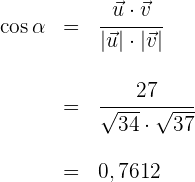
5 Der Wert  , der die vorhergehende Gleichung erfüllt, ist
, der die vorhergehende Gleichung erfüllt, ist 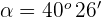
Gegeben sind die Vektoren 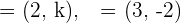 . Berechne
. Berechne  so, dass die Vektoren
so, dass die Vektoren  und
und  senkrecht aufeinander sind.
senkrecht aufeinander sind.
1 Mithilfe der Formel zur Berechnung den Winkels zwischen zwei Vektoren erhalten wir
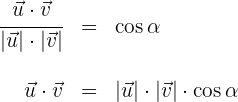
2 Wir berechnen das Skalarprodukt
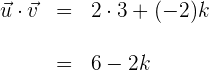
3 Zwei Vektoren sind senkrecht aufeinander, wenn der Winkel zwischen ihnen  beträgt; der Kosinus dieses Winkels ist null
beträgt; der Kosinus dieses Winkels ist null
4 Wir berechnen den Betrag des ersten Winkels
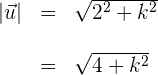
5 Wir berechnen den Betrag des zweiten Winkels

6 Wir setzen in unsere ursprüngliche Formel die vorher erhaltenen Werte ein und lösen nach  auf
auf

Der gesuchte Wert ist also 
Gegeben sind die Vektoren 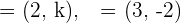 . Bereche
. Bereche  so, dass die Vektoren
so, dass die Vektoren  und
und  parallel sind.
parallel sind.
1 Mithilfe der Formel zur Berechnung den Winkels zwischen zwei Vektoren erhalten wir
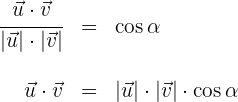
2 Wir berechnen das Skalarprodukt der Vektoren
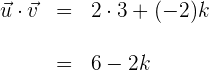
3 Zwei Vektoren sind parallel, wenn der Winkel zwischen ihnen 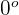 ist; der Kosinus dieses Winkels ist eins
ist; der Kosinus dieses Winkels ist eins
4 Wir berechnen den Betrag des ersten Vektors
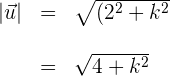
5 Wir berechnen den Betrag des zweiten Vektors

6 Wir setzen in unsere ursprüngliche Formel die vorher erhaltenen Werte ein und lösen nach  auf
auf

Der gesuchte Wert ist also 
Eine andere Möglichkeit, die Aufgabe zu lösen, besteht darin, die Proportionalität der Komponenten zu berücksichtigen

Gegeben sind die Vektoren 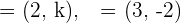 . Berechne
. Berechne  so, dass die Vektoren
so, dass die Vektoren  und
und  einen Winkel von
einen Winkel von  bilden.
bilden.
1 Mithilfe der Formel zur Berechnung den Winkels zwischen zwei Vektoren erhalten wir
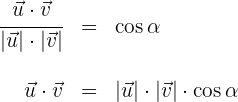
2 Wir berechnen das Skalarprodukt der Vektoren
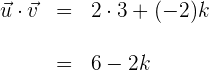
3 Der Winkel zwischen den zwei Vektoren beträgt  ; der Kosinus dieses Winkels ist
; der Kosinus dieses Winkels ist

4 Wir berechnen den Betrag des ersten Vektors
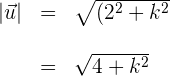
5 Wir berechnen den Betrag des zweiten Vektors

6 Wir setzen in unsere ursprüngliche Formel die vorher erhaltenen Werte ein und lösen nach  auf.
auf.

7 Wir lösen mithilfe der Formel zur Bestimmung der Nullstellen der quadratischen Gleichung

Die Nullstellen sind 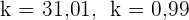 . Aber nur
. Aber nur 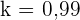 ist die Lösung von
ist die Lösung von  , da wir bereits quadriert haben, um die Lösungen zu erhalten. Der gesuchte Werte ist also
, da wir bereits quadriert haben, um die Lösungen zu erhalten. Der gesuchte Werte ist also 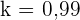 .
.
Bestimme  , wenn der Winkel, den
, wenn der Winkel, den  und
und 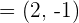 bilden,
bilden,  beträgt.
beträgt.
1 Mithilfe der Formel zur Berechnung den Winkels zwischen zwei Vektoren erhalten wir
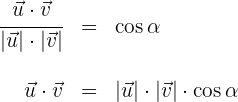
2 Wir berechnen das Skalarprodukt der Vektoren
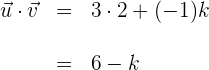
3 Der Kosinus von  ist null
ist null
4 Wir berechnen den Betrag des ersten Vektors

5 Wir berechnen den Betrag des zweiten Vektors

6 Wir setzen in unsere ursprüngliche Formel die vorher erhaltenen Werte ein und lösen nach  auf
auf

Der gesuchte Wert ist also 
Bestimme  , wenn der Winkel, den die Vektoren
, wenn der Winkel, den die Vektoren  und
und 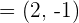 bilden,
bilden, 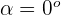 beträgt.
beträgt.
1 Mithilfe der Formel zur Berechnung den Winkels zwischen zwei Vektoren erhalten wir
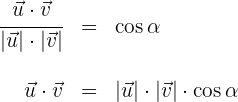
2 Wir berechnen das Skalarprodukt der Vektoren
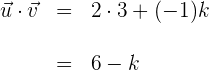
3 Der Kosinus von 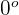 ist eins
ist eins
4 Wir berechnen den Betrag des ersten Vektors

5 Wir berechnen den Betrag des zweiten Vektors

6 Wir setzen in unsere ursprüngliche Formel die vorher erhaltenen Werte ein und lösen nach  auf
auf

Der gesuchte Wert ist also 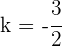
Bestimme  , wenn der Winkel, den die Vektoren
, wenn der Winkel, den die Vektoren  und
und 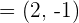 bilden,
bilden,  beträgt.
beträgt.
1 Mithilfe der Formel zur Berechnung den Winkels zwischen zwei Vektoren erhalten wir
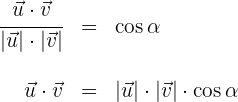
2 Wir berechnen das Skalarprodukt der Vektoren
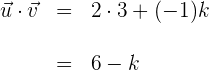
3 Der Winkel zwischen den zwei Vektoren beträgt  ; der Kosinus dieses Winkels ist
; der Kosinus dieses Winkels ist

4 Wir berechnen den Betrag des ersten Vektors
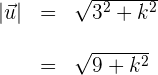
5 Wir berechnen den Betrag des zweiten Vektors

6 Wir setzen in unsere ursprüngliche Formel die vorher erhaltenen Werte ein und lösen nach  auf
auf

Die Nullstellen sind 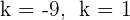
Überprüfe, ob das Segment, das die Mittelpunkte der Seiten  und
und  des Dreiecks:
des Dreiecks: 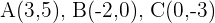 verbindet, parallel zur Seite
verbindet, parallel zur Seite  und gleich ihrer Hälfte ist.
und gleich ihrer Hälfte ist.
1 Wir stellen grafisch dar
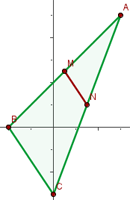
2 Wir berechnen den Mittelpunkt der Seite 

3 Wir berechnen den Mittelpunkt der Seite 
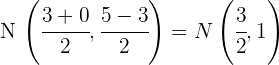
4 Wir berechnen den Vektor 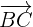
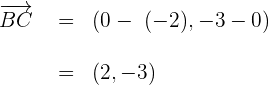
5 Wir berechnen den Vektor 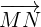
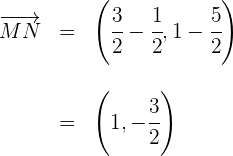
6 Wir berechnen den Betrag des ersten Vektors
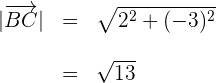
7 Wir berechnen den Betrag des zweiten Vektors
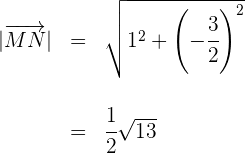
8 Um herauszufinden, ob die zwei Vektoren parallel sind, überprüfen wir die Proportionalität ihrer Komponenten

Da die Komponenten proportional sind, sind die Vektoren parallel
Berechne die Winkels des Dreiecks mit den Eckpunkten:  .
.
1 Wir stellen grafisch dar
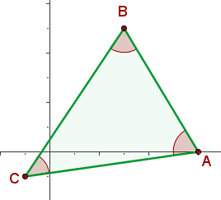
2 Wir berechnen den Vektor 
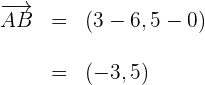
3 Wir berechnen den Vektor 

4 Wir berechnen den Betrag von 
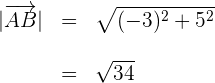
5 Wir berechnen den Betrag von 

6 Wir berechnen das Skalarprodukt der beiden Vektoren
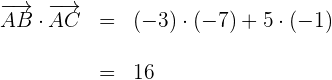
7 Wir setzen die vorher ermittelten Werte in die Formel des Winkels  zwischen zwei Vektoren ein
zwischen zwei Vektoren ein
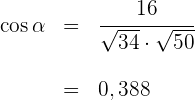
Der Wert  , der zum Eckpunkt
, der zum Eckpunkt  gehört und die vorherige Gleichung erfüllt, ist
gehört und die vorherige Gleichung erfüllt, ist 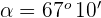
8 Wir berechnen den Vektor 
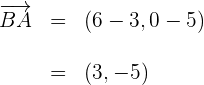
9 Wir berechnen den Vektor 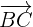
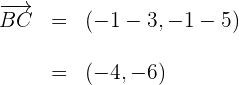
10 Wir berechnen den Betrag von 

11 Wir berechnen den Betrag von 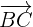

12 Wir berechnen das Skalarprodukt der beiden Vektoren

13 Wir setzen die vorher ermittelten Werte in die Formel des Winkels  zwischen zwei Vektoren ein
zwischen zwei Vektoren ein

Der Wert  , der zum Eckpunkt
, der zum Eckpunkt  gehört und die vorherige Gleichung erfüllt, ist
gehört und die vorherige Gleichung erfüllt, ist 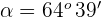
14 Da die Summe der Innenwinkel eines Dreiecks  ist, beträgt der Winkel
ist, beträgt der Winkel  des Eckpunktes
des Eckpunktes