Kapitel
Änderungsrate
Die Änderungsrate einer Funktion auf dem Intervall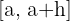 
, die mit 
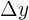angegeben wird, ist die Differenz zwischen den entsprechenden Ordinaten zu den Punkten auf der x-Achse 
und 
.
Mittlere Änderungsrate
Die mittlere Änderungsrate auf dem Intervall 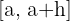, die mit 
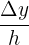oder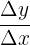 
angegeben wird, ist der Quotient aus der Änderungsrate und der Breite des betrachteten Intervalls auf der x-Achse, 
oder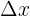 
. Das heißt:
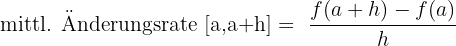
Geometrische Interpretation der mittleren Änderungsrate
Der obige Ausdruck entspricht der Steigung der Tangente an die Funktion 
, die durch die Punkte und auf der x-Achse verläuft.
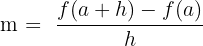
Ableitung einer Funktion in einem Punkt
Die Ableitung der Funktion im Punkt 
ist der Wert des Grenzwerts, sofern es einen gibt, eines zunehmenden Quotienten, wenn die Zunahme der Variablen gegen 0 konvergiert.
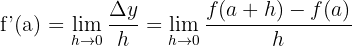
Geometrische Interpretation der Ableitung
Die Steigung der Tangente an den Graphen in einem Punkt ist gleich der Ableitung der Funktion in diesem Punkt.
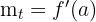
Physische Interpretation der Ableitung
Die Momentangeschwindigkeit ist der Grenzwert der Durchschnittsgeschwindigkeit, wenn Δt gegen 0 konvergiert, d. h. die Ableitung des Zeitraums in Bezug auf die Zeit.
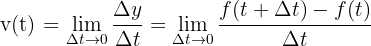
Die Ableitung
Die Ableitung der Funktion ist eine Funktion, die jeder reellen Zahl ihre Ableitung zuordnet, sofern diese existiert. Sie wird mit 
angegeben.
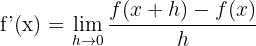
Links- und rechtsseitige Ableitungen
Linksseitige Ableitung
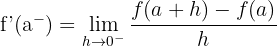
Rechtsseitige Ableitung
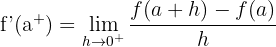
Eine Funktion ist genau dann in einem Punkt ableitbar, wenn sie links und rechts von diesem Punkt ableitbar ist und die seitlichen Ableitungen übereinstimmen.
Ableitbarkeit und Stetigkeit
Wenn eine Funktion in einem Punkt ableitbar ist, ist sie für stetig.
Das Umgekehrte ist falsch, d. h. es gibt Funktionen, die in einem Punkt stetig sind und dennoch nicht abgeleitet werden können.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
