Vektoren - wichtige Definitionen
Äquivalente Vektoren
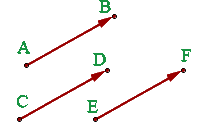
Zwei Vektoren sind äquivalent, wenn sie den gleichen Betrag und die gleiche Orientierung haben und in die gleiche Richtung zeigen.
Freie Vektoren
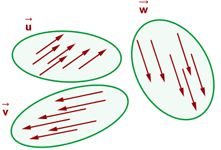
Die Menge aller äquivalenten Vektoren wird als freier Vektor bezeichnet. Das heißt, die freien Vektoren haben denselben Betrag, dieselbe Richtung und dieselbe Orientierung.
Gebundene Vektoren
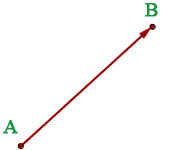
Ein gebundener Vektor ist ein Repräsentant des freien Vektors. Das heißt, gebundene Vektoren haben denselben Betrag, dieselbe Richtung, dieselbe Orientierung und denselben Ursprung.
Äquivalente Vektoren auf einer Geraden
Diese Vektoren sind äquivalent und liegen auf derselben Geraden. Das heißt, dass die gebundenen Vektoren denselben Betrag, dieselbe Richtung und dieselbe Orientierung haben und auf derselben Geraden liegen.
Gegenvektoren
Gegenvektoren haben den gleichen Betrag, die gleiche Richtung, aber entgegengesetzte Orientierung.
Einheitsvektoren
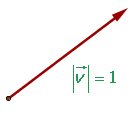
Der Betrag von Einheitsvektoren ist die Einheit. Das heißt, ein Vektor 
ist ein Einheitsvektor, wenn
Um einen Einheitsvektor mit derselben Richtung und derselben Orientierung wie der gegebene Vektor zu erhalten, teilt man den gegebenen Vektor durch seinen Betrag.
Vektoren, die denselben Anfangspunkt haben
Diese Vektoren haben denselben Anfangspunkt.
Ortsvektor
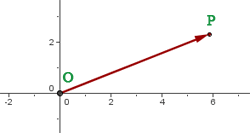
Der Vektor 
hat seinen Anfangspunkt im Ursprung 
und seinen Endpunkt im Punkt 
. Dieser Vektor wird Ortsvektor des Punktes 
genannt.
Linear unabhängige Vektoren
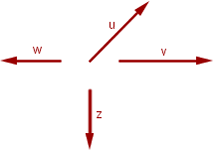
Es gibt zwei Hauptarten, diese zu definieren. Die erste Definition besagt, dass mehrere freie Vektoren in der Ebene linear unabhängig sind, wenn sich keiner von ihnen als Linearkombination der anderen ausdrücken lässt. Die zweite Defintion besagt, dass mehrere freie Vektoren der Ebene linear unabhängig sind, wenn es eine Linearkombination von ihnen gibt, die gleich dem Nullvektor ist, ohne dass alle Koeffizienten der Linearkombination null sind. Das bedeutet, dass die Vektoren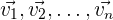 
linear unabhängig sind, wenn es reelle Zahlen 
gibt, die nicht alle null sind (mindestens eine 
)
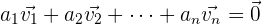
Linear abhängige Vektoren
Auch hier gibt es zwei wesentliche Definitionsmöglichkeiten. Die erste Möglichkeit besagt, dass mehrere freie Vektoren der Ebene linear abhängig sind, wenn einer als Linearkombination der anderen ausgedrückt werden kann. Zum anderen sind mehrere freie Vektoren der Ebene linear abhängig, wenn eine Linearkombination von ihnen nur dann gleich dem Nullvektor sein kann, wenn alle Koeffizienten gleich dem Skalar null sind. Das heißt, dass
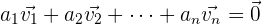
Dies gilt nur, wenn
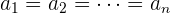
Orthogonale Vektoren
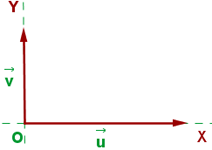
Zwei Vektoren sind zueinander orthogonal oder senkrecht, wenn deren Skalarprodukt null ist. Das heißt, die Vektoren 
und 
sind nur dann orthogonal, wenn
.
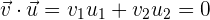Orthonormale Vektoren
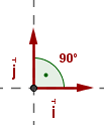
Zwei Vektoren und sind zueinander orthonormal, wenn sie Folgendes erfüllen:
-
- Sie sind zueinander orthogonal :
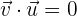
- Sie sind zueinander orthogonal :
- Sie sind Einheitsvektoren:
Beispielaufgaben zu Vektoren
1. Gegeben ist der Vektor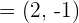 
. Bestimme zwei Vektoren äquivalent zu 
, 
und 
. 
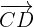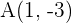und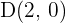 
sind gegeben.
Um diese Aufgabe zu lösen, müssen wir Folgendes beachten: ist der Ortsvektor des Punktes 
und wir beachten, dass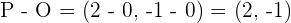 
(
ist der Ursprung). Das heißt, der Vektor ist durch die Differenz der Punkte, die er verbindet, definiert. So muss jeder Vektor, der äquivalent zu ist, die Bedingung erfüllen, dass Endpunkt minus Anfangspunkt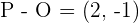 
ist. Der Anfangspunkt des Vektors ist 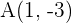und wir müssen nun den Endpunkt 
bestimmen. Wir gehen wie folgt vor
Wir erhalten 
. Nun können wir den Anfangspunkt des Vektors 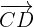bestimmen, da wir den Endpunkt 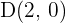kennen
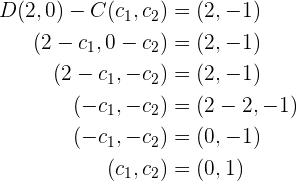
Wir erhalten also 
.
2. Berechne die Koordinaten von 
für das Viereck mit den Eckpunkten: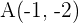 
, 
, 
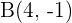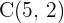und ; es handelt sich um ein Parallelogramm.
Die folgende Abbildung zeigt unser Parallelogramm
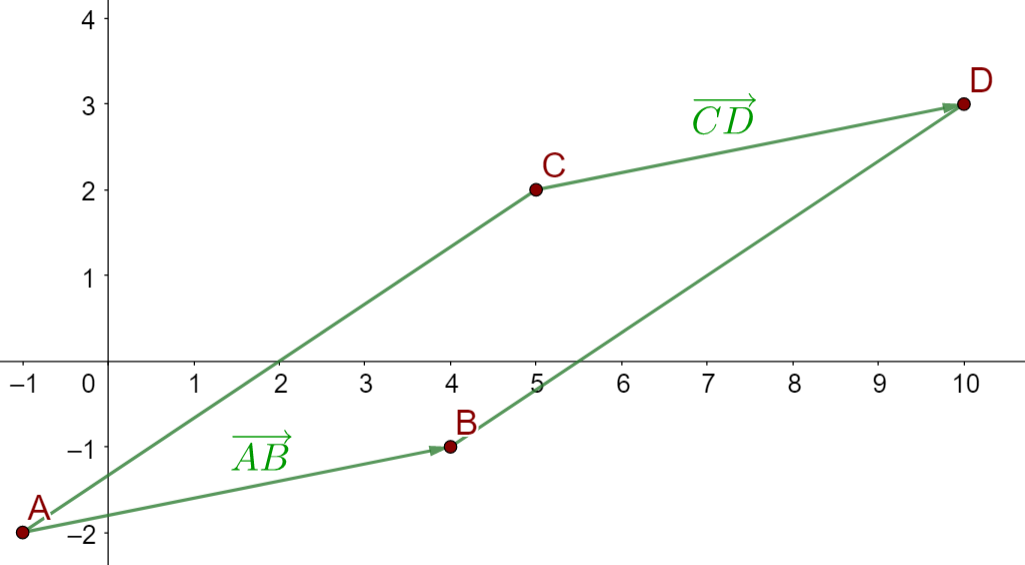
Wir müssen nun die Koordinaten von bestimmen. Hierzu gehen wir wie in der vorhergehenden Aufgabe vor. Die Vektoren und 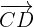müssen äquivalent sein. Deshalb gilt 
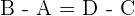und wir können so die Werte der Koordinaten des Punktes bestimmen.
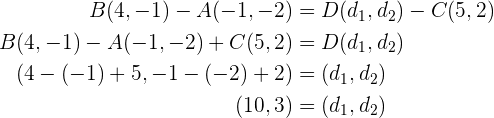
Somit ist unser Punkt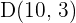 
.
3. ist ein Vektor mit den Komponenten 
. Bestimme einen Einheitsvektor mit derselben Richtung und derselben Orientierung.
Hierzu ermitteln wir zunächst den Betrag unseres Vektors
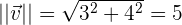
Der Vektor, den wir suchen, ist ganz einfach der Vektor geteilt durch seinen Betrag. Das heißt,
4. Bestimme einen Einheitsvektor mit derselben Richtung wie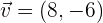 
.
Zunächst berechnen wir den Betrag unseres Vektors
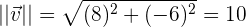
Der Vektor, den wir suchen, ist ganz einfach der Vektor geteilt durch seinen Betrag. Das heißt,
.
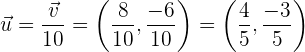Wir stellen fest, dass der Vektor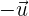 
ein Einheitsvektor ist. Er hat dieselbe Richtung, aber die entgegengesetzte Orientierung.
5. Bestimme einen Einheitsvektor 
, der dieselbe Richtung hat wie der Vektor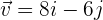 
Zunächst berechnen wir den Betrag unseres Vektors
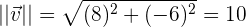
Der Vektor, den wir suchen, ist ganz einfach der Vektor geteilt durch seinen Betrag. Das heißt,
.
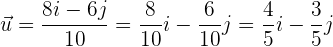Wir stellen fest, dass der Vektor 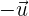ein Einheitsvektor ist. Er hat dieselbe Richtung, aber die entgegengesetzte Orientierung.
Bist du auf der Suche nach Mathe-Nachhilfe in der Nähe? Bei Superprof wirst du fündig!
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
