
Reihenfolge der Rechenoperationen
1 Rechenoperationen in geschweiften, eckigen und runden Klammern durchführen.
2 Potenzen und Wurzeln berechnen.
3 Multiplikationen und Divisionen durchführen.
4 Additionen und Subtraktionen durchführen.
Arten von kombinierten Rechenoperationen
Rechenoperationen können wie folgt eingeteilt werden, wodurch wir ihre Reihenfolge besser verstehen können:
Kombinierte Rechenoperationen ohne Klammern
1.1 Kombination aus Summen und Differenzen
Nehmen wir zum Beispiel die folgende kombinierte Rechenoperation:

Dazu beginnen wir von links und führen die Rechenoperationen so durch, wie sie erscheinen:
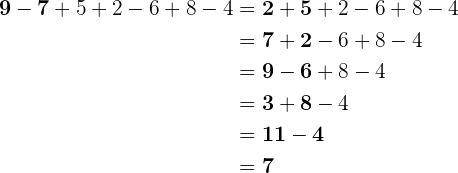
1.2 Kombination von Summen, Differenzen und Produkten
Nun betrachten wir die folgende Rechenoperation mit Multiplikationen:
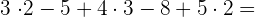
Wir führen zunächst die Produkte aus, da sie die höchste Priorität haben.
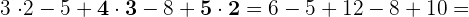
Im Anchluss addieren und subtrahieren wir (von links nach rechts).
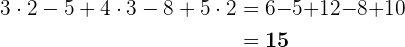
1.3 Kombination aus Summen, Differenzen, Produkten und Divisionens
Wir betrachten eine Rechenoperation mit Divisionen:
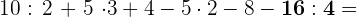
Wir führen die Multiplikationen und Divisionen in der Reihenfolge durch, wie sie erscheinen, von links nach rechts, da sie die gleiche Priorität haben.

Zuletzt addieren und subtrahieren wir, ebenfalls von links nach rechts.
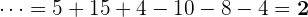
1.4 Kombination aus Summen, Differenzen, Produkten, Divisionen und Potenzen
Wir betrachten nun die folgende Rechenoperation mit Potenzen:

Als Erstes führen wir die Berechnungen mit den Potenzen durch, da sie die höchste Priorität haben.
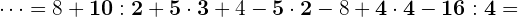
Danach multiplizieren und dividieren wir.
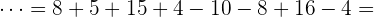
Zuletzt addieren und subtrahieren wir von links nach rechts.
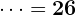
Kombinierte Rechenoperationen mit Klammern
Nun betrachten wir Rechenoperationen, in denen Klammern vorkommen. Zum Beispiel:
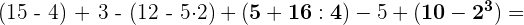
Wir führen zunächst die in den Klammern enthaltenen Rechenoperationen aus. Wir beginnen mit den Potenzen, danach folgen Multiplikation und Division:

Wir fahren mit Addition und Subtraktion innerhalb der Klammern fort. Beachte, dass wir die Klammern entfernen können, sobald wir alle Rechenoperationen innerhalb der Klammern durchgeführt haben:
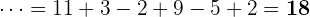
Rechenoperationen mit runden und eckigen Klammern
Schließlich betrachten wir die Rechenoperationen, bei denen alle Rechenoperationen kombiniert werden: runde Klammern, eckige Klammern, Potenzen, Multiplikationen, Divisionen, Additionen und Subtraktionen.

Zunächst arbeiten wir mit den Potenzen, Produkten und Divisionen in den Klammern.

Wir addieren und subtrahieren innerhalb der Klammern.
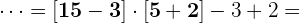
Nun sind die eckigen Klammern dran.

Wir multiplizieren.

Wir subtrahieren und addieren.

Aufgaben
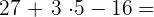
Zuerst führen wir die Multiplikationen durch, danach folgen die Additionen und Subtraktionen:
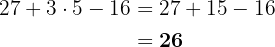
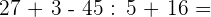
Nun dividieren wir. Im Anschluss folgen die Additionen und Subtraktionen:
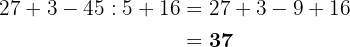
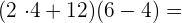
Da wir nun Klammern haben, führen wir zuerst die Rechenoperationen innerhalb dieser Klammern durch. Denk daran, die gleiche Reihenfolge der Rechenoperationen innerhalb jeder Klammer einzuhalten (d.h. wir führen die Multiplikation zuerst aus). Beachte auch, dass zwei Klammern, zwischen denen kein Malzeichen steht, eine Multiplikation bedeutet.
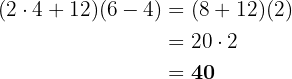

Wie in der vorherigen Aufgabe führen wir zuerst die Rechenoperationen innerhalb der Klammern aus. Danach führen wir die restlichen Rechenoperationen in ihrer normalen Reihenfolge aus:
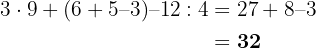
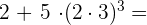
Auf die gleiche Weise müssen wir zuerst die Rechenoperationen innerhalb der Klammern durchführen. Dann führen wir die Potenzen aus, gefolgt von den Multiplikationen und schließlich den Additionen.
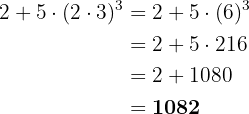

Hier müssen wir die Rechenoperationen der Klammern durchführen (da sie sich innerhalb von eckigen Klammern befinden). Dann folgen wir der üblichen Reihenfolge:
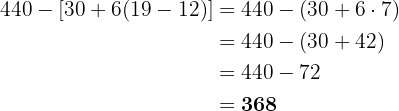

Ähnlich wie in der vorherigen Aufgabe führen wir zuerst die Rechenoperationen innerhalb der runden Klammern durch (da sie sich "ganz innen" befinden). Dann fahren wir mit den eckigen Klammern fort, da sie sich innerhalb der geschweiften Klammern befinden:
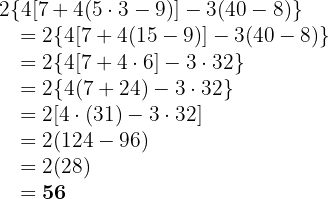
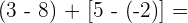
Diese Aufgabe ist den vorherigen Aufgaben sehr ähnlich. Zuerst führen wir die Rechenoperationen innerhalb der Klammern durch. Wir müssen auch beachten, dass 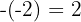 .
.
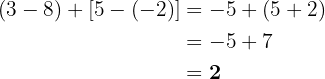
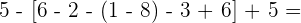
In ähnlicher Weise beginnen wir mit den Rechenoperationen innerhalb der Klammern:
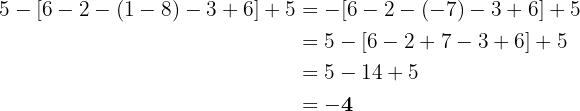
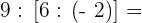
Wir beginnen mit der Division innerhalb der eckigen Klammer. Wir erinnern uns daran, dass die Division einer positiven Zahl durch eine negative Zahl eine negative Zahl ergibt.
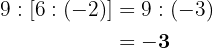

Hierbei müssen wir beachten, dass die ungerade Potenz von negativen Zahlen eine negative Zahl ist. Deshalb
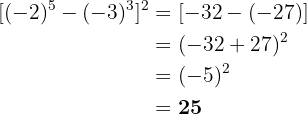

Diese Aufgabe ist den vorherigen Aufgaben sehr ähnlich. Wir beginnen mit den Rechenoperationen innerhalb der Klammern:
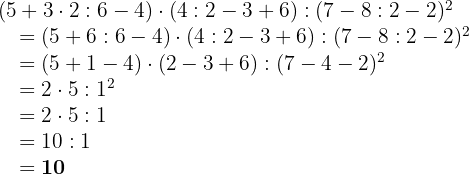

Wir gehen genauso vor wie in den vorherigen Aufgaben und beginnen mit den Rechenoperationen innerhalb der Klammern:
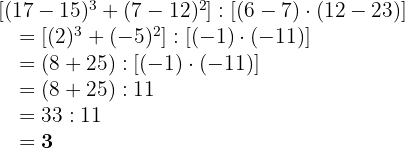
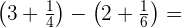
In diesem Fall addieren wir zunächst die Brüche in den Klammern. Anschließend subtrahieren wir die Brüche. Es ist wichtig, dass wir nicht mit Brüchen als Divisionen rechnen (obwohl das möglich ist, der einzige Nachteil ist, dass wir mit Dezimalstellen rechnen würden).
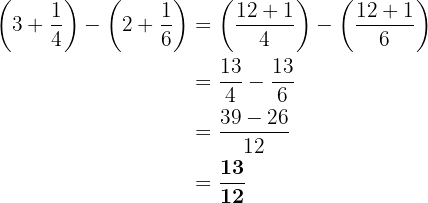
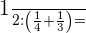
Diese Aufgabe ist ähnlich wie die vorherige Aufgabe. Zuerst addieren wir die Brüche innerhalb der Klammern, dann dividieren wir die Brüche.
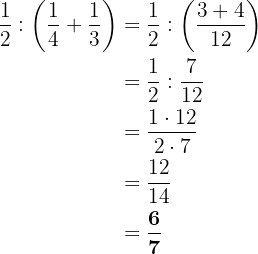
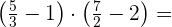
Wie in der vorherigen Übung führen wir zunächst die Subtraktionen innerhalb der Klammern durch.
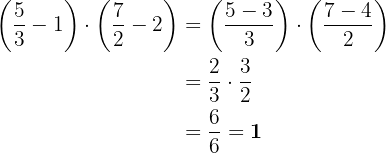
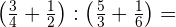
Wir beginnen mit den Summen innerhalb der Klammern:
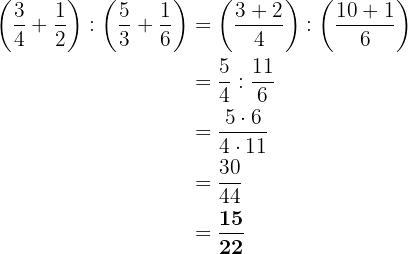

Ähnlich wie bei den vorherigen Aufgaben folgen wir der Reihenfolge, die wir zu Beginn definiert haben (beginnend mit den Rechenoperationen innerhalb der Klammern und endend mit den Additionen und Subtraktionen).
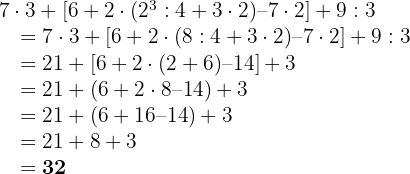
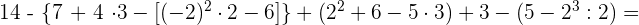
Wir führen die Rechenoperationen in der oben beschriebenen Reihenfolge durch:
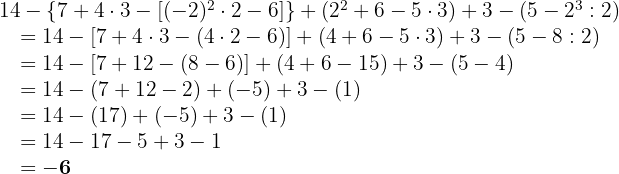
Mit KI zusammenfassen:












