
Algebraische Ausdrücke
In der Algebra geht es um den Umgang mit numerischen Beziehungen, bei denen eine oder mehrere Größen unbekannt sind. Diese Größen heißen Variablen oder Unbekannte und werden als Buchstaben dargestellt.
Ein algebraischer Ausdruck ist eine Kombination aus Buchstaben und Zahlen, mit denen bestimmte Rechenoperationen durchgeführt werden müssen: Addition, Subtraktion, Multiplikation, Division und Potenzierung.
Mit algebraischen Ausdrücken lassen sich zum Beispiel Flächen oder Volumen berechnen.
Umfang eines Kreises:  , wobei
, wobei  der Radius des Kreises ist.
der Radius des Kreises ist.
Fläche zum Quadrat:  , wobei
, wobei  die Seite des Quadrats ist.
die Seite des Quadrats ist.
Volumen eines Quaders:  , wobei
, wobei  die Kante des Quaders ist.
die Kante des Quaders ist.
Allgemeine algebraische Ausdrücke
Das Doppelte einer Zahl: 
Das Dreifache einer Zahl: 
Das Vierfache einer Zahl: 
Die Hälfte einer Zahl: 
Ein Drittel einer Zahl:
Ein Viertel einer Zahl: 
Eine Zahl ist proportional zu 2, 3, 4...: 
Eine Zahl zum Quadrat: 
Eine Zahl zum Kubik: 
Eine gerade Zahl: 
Eine ungerade Zahl: 
Zwei aufeinanderfolgende Zahlen: 
Zwei aufeinanderfolgende gerade Zahlen: 
Zwei aufeinanderfolgende ungerade Zahlen: 
Die Zahl 24 in zwei Teile zerlegen: 
Die Summe zweier Zahlen ist 24: 
Die Differenz zweier Zahlen ist 24: 
Das Produkt zweier Zahlen ist 24: 
Der Quotient zweier Zahlen ist 24: 
Beispiele:
Das Dreifache einer Zahl minus 2: 
Das Doppelte der Summe einer Zahl plus 2: 
Der fünfte Teil einer Zahl zum Kubik: 
Die Hälfte einer Zahl minus fünf hoch drei: 
Die Summe einer Zahl plus drei zum Quadrat: 
Das Doppelte einer Zahl plus deren Hälfte: 
Sieben minus das Vierfache einer Zahl: 
Eine Zahl plus das Dreifache der darauffolgenden Zahl: 
Das Dreifache einer Zahl zum Quadrat minus vier: 
Monome
Ein Monom ist ein algebraischer Ausdruck, bei der die einzigen Rechenoperationen zwischen den Variablen das Produkt und die Potenz des natürlichen Exponenten sind. 
Teile eines Monoms
1 Koeffizient
Der Koeffizient des Monoms ist die Zahl, mit der die Variablen multipliziert werden.
Beispiele:
Der Koeffizient des Monoms ist
ist 
Der Koeffizient des Monoms  ist
ist 
Der Koeffizient des Monoms  ist
ist 
Der Koeffizient des Monoms  ist
ist 
Der Koeffizient des Monoms  ist
ist 
2 Unbekannte
Unbekannte werden als Buchstaben und deren Exponenten dargestellt.
Die Unbekannte des Monoms  ist
ist 
Die Unbekannte des Monoms 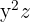 ist
ist 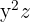
Die Unbekannte des Monoms  ist
ist 
Das Monom  hat keine Unbekannte
hat keine Unbekannte
Die Unbekannte des Monoms  ist
ist
3 Grad
Der Grad eines Monoms ist die Summe aller Exponenten der Buchstaben oder Variablen.
Der Grad des Monoms  ist:
ist: 
Der Grad des Monoms  ist:
ist: 
Der Grad des Monoms  ist:
ist: 
Der Grad des Monoms  ist:
ist:  (man kann auch
(man kann auch  schreiben)
schreiben)
Der Grad des Monoms  ist:
ist: 
Gleichartige Monome
Zwei Monome sind gleichartig, wenn die Unbekannte gleich ist.
 ist gleichartig zu
ist gleichartig zu 
 ist gleichartig zu
ist gleichartig zu 
 ist gleichartig zu
ist gleichartig zu 
Rechenoperationen mit Monomen
1. Summe von Monomen
Um zwei oder mehrere Monome zu addieren, müssen diese gleichartig sein. Das heißt, die Variablen der Monome müssen gleich sein.
Die Summe der Monome ist ein weiteres Monom, das die gleiche Variable hat und dessen Koeffizient die Summe der Koeffizienten ist.

Beispiele:



Wenn die Monome nicht gleichartig sein, erhält man bei deren Zusammenfassung ein Polynom.
Beispiel:

2. Produkt aus einer Zahl und eines Monoms
Das Produkt aus einer Zahl und einem Monom ergibt ein weiteres gleichartiges Monom, dessen Koeffizient das Produkt aus dem Koeffizienten des Monoms und der Zahl ist.
Beispiele:
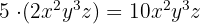
Üblicherweise lässt man das Malzeichen zwischen der Zahl und der Klammer weg

3. Multiplikation von Monomen
Die Multiplikation von Monomen ergibt ein weiteres Monom, dessen Koeffizient das Produkt aus den Koeffizienten ist. Die Variable des Monoms ist die Multiplikation der Potenzen, die die gleiche Basis haben. Man addiert also die Exponenten.

Beispiel:


4. Division von Monomen
Monome können nur dividiert werden, wenn der Grad des Dividenden größer als der des Divisors ist oder gleich
Die Division von Monomen ergibt ein weiteres Monom, dessen Koeffizient der Quotient der Koeffizienten ist. Die Unbekannte erhält man, indem man die Potenzen, die die gleiche Basis haben dividiert. Man subtrahiert also die Exponenten.

Beispiel:

Wenn der Grad des Divisors größer ist, erhalten wir einen Bruchterm.
Beispiel:

5. Potenz eines Monoms
Um ein Monom zu potenzieren, muss jeder Faktor separat potenziert werden und die Exponenten der Variablen werden mit dem Exponenten multipliziert.

Beispiel:


Mit KI zusammenfassen:













