
Was ist das Horner-Schema?
Das Horner-Schema geht auf den Mathematiker William George Horner zurück und ist ein Umformungsverfahren für Polynome. Es kann genutzt werden, um die Polynomdivision zu vereinfachen, wenn ein Polynom durch ein Binom der Form x — a geteilt werden soll.
Um die Schritte zur Durchführung des Horner-Schemas zu erklären, sehen wir uns zwei Beispiele an:
Erstes Beispiel
Dividieren: 
1 Wenn das Polynom nicht vollständig ist, schreiben wir für alle fehlenden Terme eine Null.
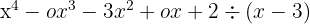
2 Wir schreiben alle Koeffizienten des Dividenden in eine Zeile.

3 Darunter schreiben wir nach links versetzt das konstante Glied des Divisors, aber mit umgedrehtem Vorzeichen: 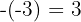 .
.


4Wir ziehen eine Linie und schreiben darunter den ersten Koeffizienten  .
.
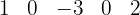
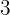

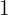
5Wir multiplizieren diesen Koeffizienten  mit dem Divisor
mit dem Divisor 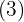 und schreiben das Ergebnis unter den zweiten Term
und schreiben das Ergebnis unter den zweiten Term 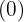 .
.
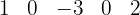


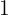
6Wir addieren die beiden Koeffizienten 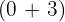 .
.
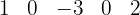



7Wir wiederholen den vorhergehenden Schritt 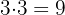 und
und 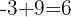 ).
).
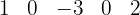



Wir wiederholen den Vorgang 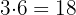 und
und 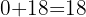 .
.
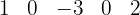


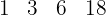
Wir wiederholen den Vorgang  und
und 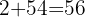 .
.
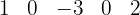



8Die letzte Zahl, die wir erhalten ist 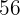 , also der Rest, der bleibt.
, also der Rest, der bleibt.
9Der Quotient ist ein Polynom, dessen Grad um eine Einheit niedriger ist als der Grad des Dividenden. Die Koeffizienten sind die, die wir erhalten haben.
Quotient: 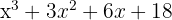
Rest: 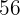
Zweites Beispiel
Dividieren mit dem Horner-Schema: 
1 Wenn das Polynom nicht vollständig ist, schreiben wir für alle fehlenden Terme eine Null.
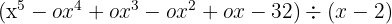
2Wir schreiben alle Koeffizienten des Dividenden in eine Zeile.
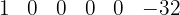
3Darunter schreiben wir nach links versetzt das konstante Glied des Divisors, aber mit umgedrehtem Vorzeichen: 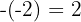 .
.


4Wir ziehen eine Linie und schreiben darunter den ersten Koeffizienten  .
.



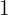
5Wir multiplizieren diesen Koeffizienten  mit dem Divisor
mit dem Divisor  und schreiben das Ergebnis unter den darauffolgenden Term
und schreiben das Ergebnis unter den darauffolgenden Term 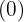 .
.



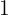
6Wir addieren die beiden Koeffizienten  .
.




7 Wir wiederholen die Schritte  und
und  bis zum Ende.
bis zum Ende.

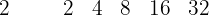

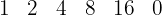
8 Der Quotient ist ein Polynom, dessen Grad um eine Einheit niedriger ist als der Grad des Dividenden. Die Koeffizienten sind die, die wir erhalten haben.
Quotient: 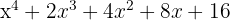
Rest: 
Mit KI zusammenfassen:













