Kapitel
Wenn es um die Faktorisierung von Polynomen geht, müssen wir dabei einige Dinge beachten.

Wenn es kein konstantes Glied gibt
Wenn es kein konstantes Glied gibt, muss ein gemeinsamer Faktor ausgeklammert werden. Um einen gemeinsamen Faktor bei einer Summe (oder Differenz) auszuklammern, muss in ein Produkt umgeformt werden.
Wir wenden das Distributivgesetz an:
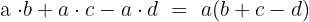
Beispiel für die Faktorisierung eines Polynoms ohne konstantes Glied
Wir zerlegen in Faktoren, indem wir einen gemeinsamen Faktor ausklammern und bestimmen die Nullstellen.
1 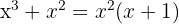
Die Nullstellen sind:  und
und 
2 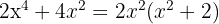
Es gibt nur eine Nullstelle  , da das Polynom
, da das Polynom  keinen Wert hat, für den es null wird. Da
keinen Wert hat, für den es null wird. Da  zum Quadrat steht, ist das Ergebnis immer eine positive Zahl und somit irreduzibel.
zum Quadrat steht, ist das Ergebnis immer eine positive Zahl und somit irreduzibel.
Zweifaches Ausklammern des gemeinsamen Faktors
1 
Wir klammern den gemeinsamen Faktor  und
und  aus.
aus.
Da  nun ein gemeinsamer Faktor ist, klammern wir den gemeinsamen Faktor
nun ein gemeinsamer Faktor ist, klammern wir den gemeinsamen Faktor  aus.
aus.

Die Nullstellen sind  und
und  .
.
Wenn es sich um ein Binom handelt
Wenn wir ein Binom haben, kann einer der folgenden Fälle auftreten:
Differenz von Quadraten
Eine Differenz von Quadraten entspricht Summe mal Differenz.

Beispielaufgaben zur Differenz von Quadraten:
In Faktoren zerlegen und Nullstellen bestimmen
1 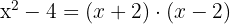
Die Nullstellen sind  und
und 
2 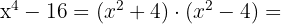
Der letzte Term ist ebenfalls eine Differenz von Quadraten. Somit gilt:
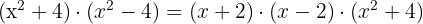
Die Nullstellen sind  und
und 
Summe von Kubikzahlen
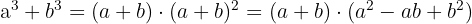
Beispielaufgabe zur Summe von Kubikzahlen:

Differenz von Kubikzahlen
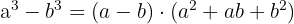
Beispielaufgabe zur Differenz von Kubikzahlen:
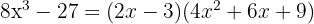
Wenn es sich um ein Trinom handelt
Wenn wir ein Trinom haben, kann einer der folgenden Fälle auftreten
Ein vollständiges quadratisches Trinom
Ein vollständiges quadratisches Trinom entspricht einem Binom zum Quadrat.
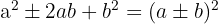
Beispiele für vollständige quadratische Trinome
In Faktoren zerlegen und Nullstellen bestimmen
1 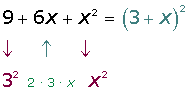
Wir müssen uns folgende Fragen stellen:
- Welche Zahl zum Quadrat ergibt
 ? Die Antwort ist
? Die Antwort ist  .
. - Welche Zahl zum Quadrat ergibt
 ? Die Antwort ist
? Die Antwort ist  .
.
Wir überprüfen: 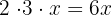
Die Nullstelle ist  , in diesem Fall eine doppelte Nullstelle
, in diesem Fall eine doppelte Nullstelle
2 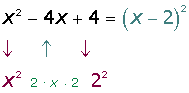
- Welche Zahl zum Quadrat ergibt
 ?
? 
- Welche Zahl zum Quadrat ergibt
 ?
? 
Wir überprüfen: 
Die doppelte Nullstelle ist  .
.
Ein Trinom zweiten Grades
Um ein Trinom zweiten Grades 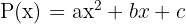 in Faktoren zu zerlegen, setzt man es gleich null und löst die Gleichung zweiten Grades.
in Faktoren zu zerlegen, setzt man es gleich null und löst die Gleichung zweiten Grades.
Wenn die Lösungen der Gleichung  und
und  sind, sieht das faktorisierte Polynom wie folgt aus:
sind, sieht das faktorisierte Polynom wie folgt aus:

Beispiele zu Trinomen zweiten Grades
In Faktoren zerlegen und Nullstellen bestimmen
1 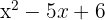
Wir setzen das Trinom gleich null

Wir wenden die Formel zur Lösung von Gleichungen zweiten Grades an:
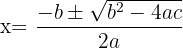
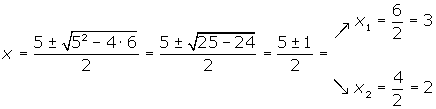
Wir faktorisieren
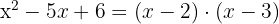
Die Nullstellen sind  und
und  .
.
2 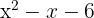
Wir setzen das Trinom gleich null

Wir lösen die Gleichung
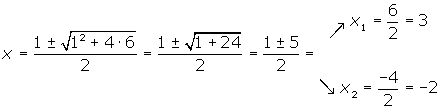
Wir faktorisieren

Die Nullstellen sind  und
und  .
.
Trinome vierten Grades mit geradzahligen Exponenten
Um die Nullstellen zu bestimmen, setzen wir gleich null und lösen die biquadratische Gleichung.
Beispiele zu Trinomen vierten Grades mit geradzahligen Exponenten
1 
Wir setzen das Polynom gleich null

Wir substituieren die Variable
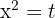
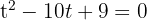
Wir lösen die Gleichung zweiten Grades
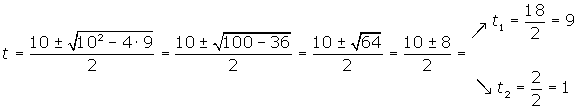
Wir führen die Rücksubstitution durch und erhalten die Nullstellen
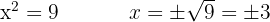

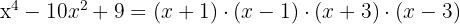
2 
Wir setzen das Polynom gleich null

Wir substituieren
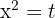
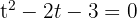
Wir lösen die Gleichung zweiten Grades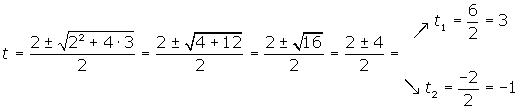
Wir führen die Rücksubstitution durch und erhalten die Nullstellen

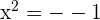 , es gibt keine reellen Nullstellen, da keine Zahl existiert, die zum Quadrat negativ ist
, es gibt keine reellen Nullstellen, da keine Zahl existiert, die zum Quadrat negativ ist
Faktorisierte Form 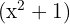
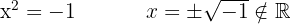
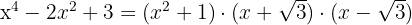
Faktorisierung eines Polynoms, das einen höheren Grad als zwei hat
Wir wenden den Restsatz und das Horner Schema an, um die Nullstellen zu bestimmen.
Sehen wir uns folgendes Polynom an:

Wir nehmen die Teiler des konstanten Glieds: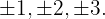
Wir wenden den Restsatz an und wissen somit, dass bei der Division kein Rest bleibt.
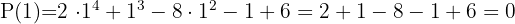
Wir wenden das Horner Schema an.
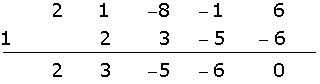
Da kein Rest bleibt, gilt 
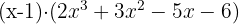
Eine Nullstelle ist  .
.
Um den zweiten Faktor zu bestimmen, führen wir die gleichen Rechenschritte durch.
Wir probieren mit  , da der erste Faktor zum Quadrat stehen könnte.
, da der erste Faktor zum Quadrat stehen könnte.

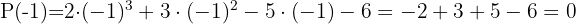
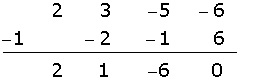

Die andere Nullstelle ist  .
.
Den dritten Faktor können wir bestimmen, indem wir die Gleichung zweiten Grades anwenden.
Die  schließen wir aus und probieren weiter mit
schließen wir aus und probieren weiter mit  .
.
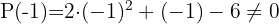
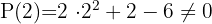

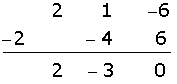
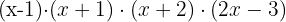
Wir klammern den gemeinsamen Faktor  im letzten Binom aus und erhalten eine rationale Nullstelle.
im letzten Binom aus und erhalten eine rationale Nullstelle.
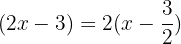
Die Faktorisierung des Polynoms sieht wie folgt aus:
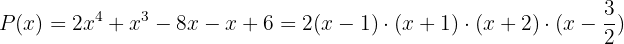

Rationale Nullstellen
Es kann vorkommen, dass das Polynom keine ganzzahligen Nullstellen hat, sondern nur rationale Nullstellen. In diesem Fall nehmen wir die Divisoren des konstanten Glieds geteilt durch die Divisoren des Terms mit dem höheren Grad und wenden den Restsatz und das Horner Schema an.

Wir probieren mit:
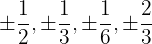 .
.

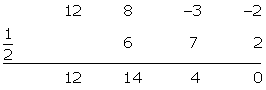
Wir faktorisieren. 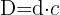
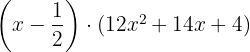
Wir probieren noch einmal mit 

Wir probieren mit 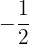
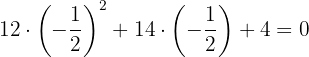
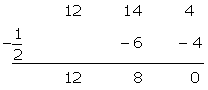
Wir faktorisieren: 
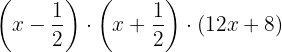
Wir klammern den gemeinsamen Faktor  im dritten Faktor aus.
im dritten Faktor aus.
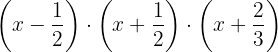
Mit KI zusammenfassen:













