Kapitel
In diesem Artikel befassen wir uns mit der Faktorisierung von Polynomen. Zuerst sehen wir uns einige Gesetze und Regeln für den Umgang mit Polynomen an. Diese helfen uns dabei, Polynome auf einfache Art und Weise zu faktorisieren. Außerdem sehen wir uns die möglichen Methoden zur Faktorisierung genauer an. Zum Schluss üben wir noch anhand von einigen Beispielen, wie Polynome faktorisiert werden.
Gesetze zu den Faktoren eines Polynoms
Um die folgenden Gesetze zu verstehen, denken wir daran, dass 
eine Nullstelle des Polynoms 
ist, wenn die Bedingung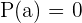 
erfüllt ist.
Der Restsatz
Satz: Der Rest, der bei der Division eines Polynoms durch ein Polynom der Form 
bleibt, entspricht dem Ergebnis, das man erhält, wenn in das Polynom eingesetzt wird.
Wenn wir zum Beispiel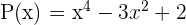 
durch 
mithilfe des Horner Schemas dividieren:
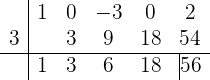
Somit ist der Quotient der Division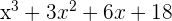 
, während ein Rest von 56 bleibt. Wenn wir aber für 3 berechnen, erhalten wir:
Merke: Wenn gilt 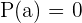, bedeutet das, dass der Rest 0 ist. Anders gesagt:
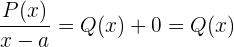
Wenn wir beide Seiten mit multiplizieren, gilt
Deshalb ist ein Faktor von . Dieses Ergenis ist als Restsatz bekannt.
Restsatz
Satz: Das Polynom ist teilbar durch ein Polynom der Form , aber nur wenn gilt .
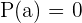Sehen wir uns als Beispiel das Polynom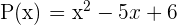 
an. Wir stellen fest, dass
deshalb gilt 
. Außerdem sind 
und 
Nullstellen von .
Merke: Wenn ein Polynom vom Grad 
und teilbar durch ist, hat das Ergebnis folgende Form:
ist hierbei die Konstante und der sogenannte Rest, der bleibt. 
ist ein Polynom vom Grad 
.
Fundamentalsatz der Algebra
Satz: Ein Polynom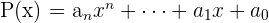 
vom Grad und mit reellen Koeffizienten 
hat genau Nullstellen. Diese können reelle oder komplexe Zahlen sein.
Merke: Reelle Polynome haben Nullstellen. Allerdings kann es vorkommen, dass keine Nullstelle reell ist. Wenn es keine reelle Nullstelle gibt, kann das Polynom nicht in Linearfaktoren zerlegt werden.
Merke: Wir denken daran, dass die Zerlegung eines Polynoms in Linearfaktoren bedeutet, dass man wie folgt schreiben muss
wobei 
die Nullstellen von sind.
Satz über rationale Nullstellen
Satz: Ein Polynom 
mit den Koeffizienten 
, welche ganze Zahlen sind. Wenn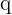 
eine rationale Nullstelle von ist, muss 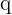folgende Form haben
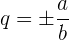
wobei ein Faktor von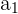 
und 
ein Faktor von 
ist.
Merke: Dieser Satz, zusammen mit dem Faktorsatz, helfen uns dabei, Nullstellen schnell zu bestimmen. Als Erstes schreiben wir alle möglichen rationalen Nullstelle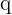n von auf. Danach überprüfen wir 
. Wenn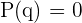 
, wissen wir, dass 
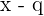ein Faktor von ist. Hierzu finden wir einige Beispiele im Beispielabschnitt.
Merke: Dieser Satz zeigt uns nur die Form der rationalen Nullstellen. Es kann vorkommen, dass ein Polynom keine rationale Nullstelle hat, wie im Fall von 
, dessen Nullstellen 
und 
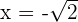sind.
Merke: Wenn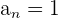 
, dann ist das Polynom ein normiertes Polynom. In diesem Fall ist 1 der einzige Faktor von . Deshalb haben die Nullstellen folgende Form
ist hierbei ein Faktor von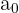 
.
Einige Regeln für Nullstellen und Faktoren eines Polynoms
1 Zu jeder Nullstelle 
gehört ein Binom vom Typ als Faktor.
2 Wir gehen davon aus, dass eine Nullstelle von ist. Deshalb können wir wie folgt schreiben
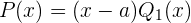
wobei 
ein Polynom vom Grad ist. Wenn wir danach feststellen, dass auch eine Nullstelle von ist, können wir wie folgt schreiben
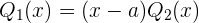
Deshalb kann wie folgt geschrieben werden
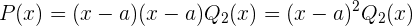
Wenn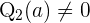 
, nehmen wir an, dass eine doppelte Nullstelle von ist. Dies bedeutet, dass die Nullstellen des Polynoms nicht unbedingt unterschiedlich sind.
3 Wir können ein Polynom faktorisiert darstellen, indem wir es als Produkt aller Binome vom Typ schreiben, zu denen die Nullstellen des Polynoms gehören. Somit wird wie folgt faktorisiert
Da zum Beispiel und Nullstellen des Polynoms 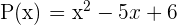sind, können wir wie folgt schreiben
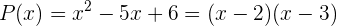
4 Jedes Polynom mit konstantem Glied hat die Nullstelle 
. Deshalb ist auch 
ein Faktor (also 
).
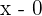Zum Beispiel kann man das Polynom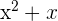 
als 
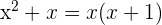faktorisieren. Deshalb kommen wir zu dem Schluss, dass die Nullstellen und 
sind.
5 Ein Polynom ist irreduzibel, wenn es nicht in Faktoren zerlegt werden kann.
Zum Beispiel kann das Polynom 
nicht faktorisiert werden und die Nullstellen sind komplex.
Methoden zur Faktorisierung eines Polynoms
Gemeinsamer Faktor
Einen gemeinsamen Faktor kann man durch Anwendung des Distributivgesetzes für reelle Zahleln ausklammern:
Sehen wir uns zum Beispiel das Polynom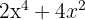 
an. Wir stellen fest, dass jeder Term teilbar durch 
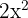ist (also ist das der gemeinsame Faktor). Somit können wir das Polynom wie folgt faktorisieren
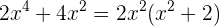
Wir stellen fest, dass das Polynom 
nicht faktorisiert werden kann, es kann also nicht weiter zerlegt werden. Die einzige Nullstelle des Polynoms ist .
Binomische Formeln
Es gibt einige Polynome zweiten Grades, die man ganz einfach faktorisieren kann, da ihre Struktur auf den ersten Blick erkennbar ist. Die gängigsten sind:
1 3. binomische Formel: Ein Polynom der Form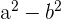 
kann wie folgt faktorisiert werden 
.
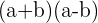Beispiel: die Polynome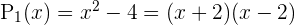 
oder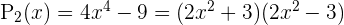 
.
2 Vollständiges quadratisches Trinom: Ein Polynom hat die Form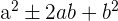 
, also können wir es wie folgt faktorisieren 
.
Sehen wir uns zum Beispiel das Polynom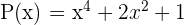 
an (hierbei gilt 
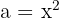und 
). Es kann wie folgt faktorisiert werden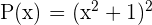 
.
Merke: Es gibt noch weitere binomische Formeln, wie zum Beispiel ein vollständiges Binom zum Kubik. Allerdings kommen diese nicht sehr häufig vor.
Mit dem Satz über rationale Nullstellen
Wenn es keinen gemeinsamen Faktor gibt oder das Polynom nicht mithilfe der binomischen Formeln faktorisiert werden kann, können wir es mit dem Satz über rationale Nullstellen versuchen (immer wenn all die Koeffizienten des Polynoms ganze Zahlen sind). Wir probieren für das Polynom alle möglichen rationalen Nullstellen 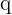und suchen, bis die Bedingung 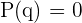erfüllt wird. In diesem Fall wenden wir das Horner Schema an, um folgende Faktorisierung durchzuführen:
Wir wiederholen mit (aber verwerfen die Faktoren 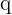, da wir wissen, dass sie keine Faktoren sind).
Die abc-Formel
Wenn es sich um ein Polynom vom Grad 2 (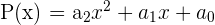
) handelt und die vorhergehenden Methoden kein Ergebnis liefern, können wir die abc-Formel anwenden:
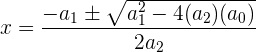
So erhalten wir die zwei Nullstellen des Polynom 
und 
und wir können das Polynom wie folgt faktorisieren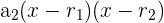 
.
Merke: Sind die Nullstellen komplex, können wir das Polynom ohne Faktorisierung stehen lassen und sagen, dass das Polynom irreduzibel ist. Es ist auch möglich, mit den komplexen Nullstellen zu faktorisieren. Allerdings sind die Faktoren in diesem Fall Polynome mit komplexen Zahlen.
Merke: Wenn das Polynom einen höheren Grad als 2 hat, liefern die vorhergehenden Methoden kein Ergebnis. Dann ist es möglich, dass alle Nullstellen irrational oder komplex sind. Um das Polynom zu faktorisieren sollte man in diesem Fall ein numerisches Verfahren anwenden oder ein Computerprogramm nutzen.
Beispiele
Finde die Nullstellen des Polynoms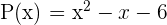 
und faktorisiere es.
Durch den Satz über rationale Nullstellen wissen wir, dass die rationalen Nullstellen die Form 
haben. Daher ist das Polynom normiert und das konstante Glied ist 6. Dessen Faktoren sind 1, 2, 3 und 6 (alle Faktoren, nicht nur die Primzahlen).
Wenn wir diese 8 möglichen Werte in das Polynom einsetzen, erhalten wir 
, 
, 
, 
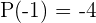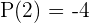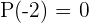(daher wissen wir, dass 
eine Nullstelle ist), 
(daher wissen wir, dass auch eine Nullstelle ist und wir müssen keine weiteren Nullstellen suchen, da wir bereits zwei gefunden haben).
Deshalb können wir das Polynom wie folgt faktorisieren
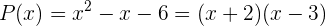
Faktorisiere die folgenden Polynome mithilfe der abc-Formel:
a 
b 
c 
Hier wenden wir für jedes Polynom die abc-Formel an:
a Als Erstes haben wir ,
deshalb ist eine Nullstelle 
und die andere Nullstelle ist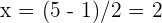 
. Daher können wir das Polynom wie folgt faktorisieren
b Für haben wir
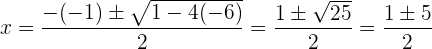
deshalb ist eine Nullstelle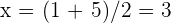 
und die andere Nullstelle ist 
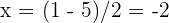. Daher können wir das Polynom wie folgt faktorisierien
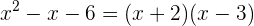
c Als letztes Beispiel haben wir . Wir stellen fest, dass es kein Polynom zweiten Grades ist. Allerdings haben wir nur die Potenzen 2 und 4 und können somit die Substitution durchführen 
,
Wir erhalten ein Polynom zweiten Grades und können die abc-Formel anwenden
Wir erhalten die Nullstellen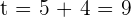 
und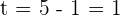 
. Allerdings gilt 
und wir erhalten somit
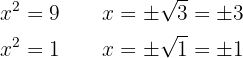
Somit hat das faktorisierte Polynom die folgende Form
Faktorisiere das folgende Polynom vierten Grades:
Da es sich um ein Polynom vierten Grades mit geraden Koeffizienten handelt, wenden wir den Satz über rationale Nullstellen an, um alle möglichen rationalen Nullstellen zu bestimmen.
Der Leitkoeffizient ist 2, dessen Faktoren sind 1 und 2. Das Absolutglied ist 6 und hat die Faktoren 1, 2, 3 und 6. Somit sind die möglichen Nullstellen
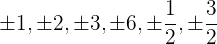
Wir verwerfen 
, da es 
entspricht; ebenso verwerfen wir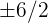 
, da es 
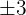entspricht.
Nun setzen wir diese Werte in das Polynom ein, um die Nullstellen zu bestimmen:
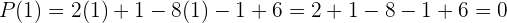
Wir stellen fest, dass 
eine Nullstelle ist. Wir wenden das Horner Schema an:
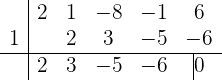
Das heißt, 
und 
sind Faktoren.
Wir gehen wie bisher vor und suchen für mögliche Nullstellen (wir versuchen es mit 1, für den Fall, dass die Nullstelle mehrfach ist):
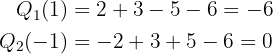
deshalb ist auch eine Nullstelle. Wir wenden nochmal das Horner Schema an:
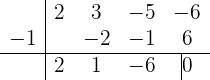
Die Faktoren sind 
und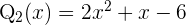 
.
Wir stellen fest, dass der letzte Faktor quadratisch ist und können deshalb die abc-Formel anwenden:
Wir erhalten die Nullstellen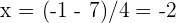 
und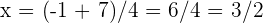 
.
Das heißt, es gibt vier Nullstellen
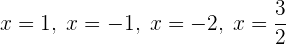
Schließlich kann das Polynom wie folgt faktorisiert werden (den Leitkoeffizienten klammern wir immer aus den Linearfaktoren aus):
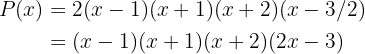
Wir multiplizieren den letzten Faktor mit 2, um den Bruch umzuwandeln.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
