Zahlenwert eines Polynoms
Der Zahlenwert eines Polynoms ist das Ergebnis, das wir erhalten, wenn wir die Variable 
durch eine gegebene Zahl ersetzen. Dies bedeutet, dass der Zahlenwert von der Zahl, die wir für unsere Variable einsetzen, abhängt. Sehen wir uns folgende Beispiele an:
Berechne den Zahlenwert des Polynoms 
für folgende Werte
a 
b 
c 
Berechne den Zahlenwert des Polynoms
für folgende Werte
a
Laut Definition müssen wir das Polynom für berechnen und erhalten somit
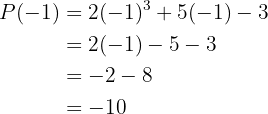
b
Wir berechnen für
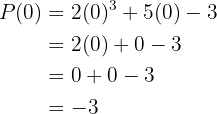
c
Schließlich berechnen wir für
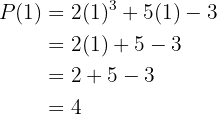
So erhalten wir drei Werte für unser Polynom 
: Der Wert von für ist 
, der Wert von für ist 
und schließlich der Wert von für ist 
.
Gleiche Polynome
Damit zwei Polynome gleich sind, müssen sie folgende Bedingungen erfüllen:
- Die beiden Polynome haben den gleichen Grad.
- Die Monome mit dem gleichen Grad müssen die gleichen Koeffizienten bei beiden Polynomen haben (sowie das gleiche Vorzeichen).
Zum besseren Verständnis sehen wir uns einige Beispiele an:
Bestimme, ob die folgenden Polynome gleich sind oder nicht und erkläre, warum.
1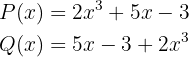 
2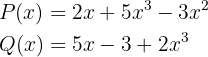 
3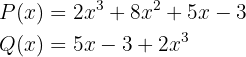 
4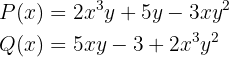 
Laut Definition müssen beide Bedingungen erfüllt sein, damit die Polynome als gleich gelten. Allerdings reicht es aus, herauszufinden, dass eine Bedingung nicht erfüllt ist, um zu beweisen, dass die Polynome nicht gleich sind.
1 Die Polynome
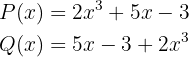
Wir stellen fest, dass der Grad der Polynome gleich ist (Grad 3). Außerdem taucht jedes Monom von auch in 
auf und die Koeffizienten stimmen überein. Deshalb sind die beiden Polynome gleich.
2 Die Polynome
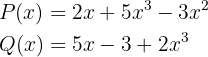
Sie sind nicht gleich, da das Monom vom Grad 
in 
ist, während das Monom vom Grad in 
ist. Somit stimmen die Koeffizienten nicht überein, nämlich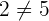 
.
3 Die Polynome
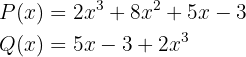
Sie sind nicht gleich, da das Monom vom Grad 
in 
ist, während in das Monom vom Grad nicht auftaucht. Das heißt, es entspricht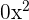 
. Somit stimmen die Koeffizienten nicht überein.
4 Die Polynome
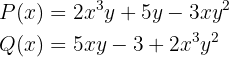
Bei diesem Beispiel haben wir Monome, in denen mehr als eine Variable vorkommt. Damit die Polynome gleich sind, müssen die Variablen in jedem Monom mit Unbekannten die gleiche Hochzahl haben. Wir stellen fest, dass das Monom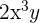 
in vorkommt, jedoch nicht in . Wir sehen, dass in dieses Monom 
ist und somit die Koeffizienten nicht übereinstimmen. Die Polynome sind also nicht gleich.
Gleichartige Polynome
Die Polynome und sind gleichartig, wenn sich für jedes Monom in ein Monom mit den gleichen Unbekannten in findet, dessen Koeffizient ungleich 
ist. Hierbei müssen die Monome nicht die gleichen Koeffizienten haben, aber die Koeffizienten dürfen nicht null sein (ungleich null).
Um diese Definition besser zu verstehen, sehen wir uns ein paar Beispiele an:
Bestimme, ob folgende Polynome gleichartig sind oder nicht und erkläre, warum.
1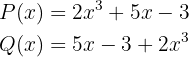
2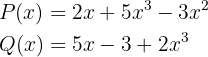
3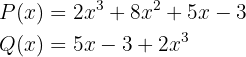
4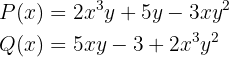
Damit die Polynome gleichartig sind, muss gelten: Wenn ein Monom in einem der Polynome vorkommt, muss ein weiteres Monom mit den gleichen Unbekannten und dem Koeffizienten ungleich null in dem anderen Polynom vorkommen.
1 Die Polynome
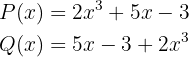
Da diese Polynome gleich sind, kommt jedes Monom des ersten Polynoms auch im zweiten Polynom vor und deswegen sind die Polynome gleichartig. Polynome, die gleich sind, sind somit immer gleichartig.
2 Die Polynome
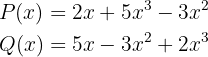
Diese Polynome sind gleichartig, da beide aus Monomen vom Grad , und 
bestehen. Die Unbekannte ist und die Koeffizienten ungleich null.
3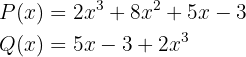
Die Polynome sind nicht gleichartig, das das Monom vom Grad in ist. In kommt das Monom vom Grad allerdings nicht vor. Somit entspricht das Monom 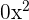und die Definition von gleichartigen Polynomen ist nicht erfüllt.
4 Die Polynome
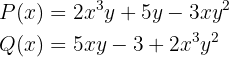
In diesem Beispiel haben wir Monome, in denen die Unbekannten aus mehreren Variablen bestehen. Wir sehen fast auf den ersten Blick, dass die Polynome nicht gleichartig sind, da wir in ein Monom vom Grad mit der Unbekannten 
haben, nämlich 
. Allerding kommt in kein Monom vom Grad mit der Unbekannten vor und die Definition von gleichartigen Polynomen ist somit nicht erfüllt.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
