Kapitel

Addition von Monomen
Um zwei oder mehr Monome addieren zu können, müssen diese gleichartig sein. Das heißt, ihre Variablen gleich sein.
Die Summe von Monomen ergibt ein weiteres Monom, das die gleichen Variablen hat und dessen Koeffizient die Summe der Koeffizienten ist.

Beispiele:



Wenn die Monome nicht gleichartig sind, ergibt die Addition der Monome ein Polynom.
Beispiel:
 können nicht addiert werden.
können nicht addiert werden.
Produkt aus einer Zahl und einem Monom
Das Produkt aus einer Zahl und einem Monom ist ein weiteres gleichartiges Monom, dessen Koeffizient das Produkt aus dem Koeffizienten des Monoms und der Zahl ist.
Beispiele:
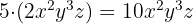
Es ist üblich, dass wir zur Angabe der Multiplikation das Zeichen „mal“ nicht zwischen die Zahl und die Klammer setzen
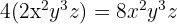
Multiplikation von Monomen
Die Multiplikation von Monomen ergibt ein weiteres Monom, dessen Koeffizient das Produkt der Koeffizienten ist und dessen Variablen sich aus der Multiplikation der Potenzen mit gleicher Basis ergeben, d. h. aus der Addition der Exponenten.

Beispiele:
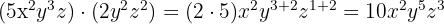
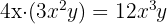
Division von Monomen
Monome können nur geteilt werden, wenn der Grad des Dividenden größer oder gleich dem des Divisors ist.
Die Division von Monomen ergibt ein weiteres Monom, dessen Koeffizient der Quotient der Koeffizienten ist und dessen Variablen sich aus der Division der Potenzen mit gleicher Basis ergeben, d. h. durch Subtraktion der Exponenten.
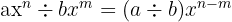
Beispiel:

Wenn der Grad des Divisors größer ist, erhalten wir einen algebraischen Bruch.
Beispiel:
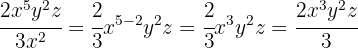
Potenz eines Monoms
Zur Potenzierung eines Monoms wird jedes Element des Monoms auf den durch die Potenz angegebenen Exponenten erhöht.

Beispiele:
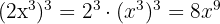

Mit KI zusammenfassen:












